题目内容
(2013•山东)设函数f(x)=
+c(e=2.71828…,c∈R).
(1)求f(x)的单调区间及最大值;
(2)讨论关于x的方程|lnx|=f(x)根的个数.
| x | e2x |
(1)求f(x)的单调区间及最大值;
(2)讨论关于x的方程|lnx|=f(x)根的个数.
分析:(1)利用导数的运算法则求出f′(x),分别解出f′(x)>0与f′(x)<0即可得出单调区间及极值与最值;
(2)分类讨论:①当0<x≤1时,令u(x)=-lnx-
-c,②当x≥1时,令v(x)=lnx-
-c.利用导数分别求出c的取值范围,即可得出结论.
(2)分类讨论:①当0<x≤1时,令u(x)=-lnx-
| x |
| e2x |
| x |
| e2x |
解答:解:(1)∵f′(x)=
=
,解f′(x)>0,得x<
;解f′(x)<0,得x>
.
∴函数f(x)的单调递增区间为(-∞,
);单调递减区间为(
,+∞).
故f(x)在x=
取得最大值,且f(x)max=
+c.
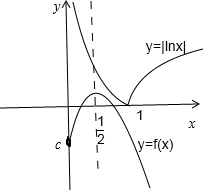
(2)函数y=|lnx|,当x>0时的值域为[0,+∞).如图所示:
①当0<x≤1时,令u(x)=-lnx-
-c,
c=-lnx-
=g(x),
则g′(x)=-
-
=-
.
令h(x)=e2x+x-2x2,则h′(x)=2e2x+1-4x>0,∴h(x)在x∈(0,1]单调递增,
∴1=h(0)<h(x)≤h(1)=e2-1.
∴g′(x)<0,∴g(x)在x∈(0,1]单调递减.
∴c≥g(1)=-
.
②当x≥1时,令v(x)=lnx-
-c,得到c=lnx-
=m(x),
则m′(x)=
-
=
>0,
故m(x)在[1,+∞)上单调递增,∴c≥m(1)=-
.
综上①②可知:当c<-
时,方程|lnx|=f(x)无实数根;
当c=-
时,方程|lnx|=f(x)有一个实数根;
当c>-
时,方程|lnx|=f(x)有两个实数根.
| e2x-x•2e2x |
| (e2x)2 |
| 1-2x |
| e2x |
| 1 |
| 2 |
| 1 |
| 2 |

∴函数f(x)的单调递增区间为(-∞,
| 1 |
| 2 |
| 1 |
| 2 |
故f(x)在x=
| 1 |
| 2 |
| 1 |
| 2e |
(2)函数y=|lnx|,当x>0时的值域为[0,+∞).如图所示:
①当0<x≤1时,令u(x)=-lnx-
| x |
| e2x |
c=-lnx-
| x |
| e2x |
则g′(x)=-
| 1 |
| x |
| 1-2x |
| e2x |
| e2x+x-2x2 |
| xe2x |
令h(x)=e2x+x-2x2,则h′(x)=2e2x+1-4x>0,∴h(x)在x∈(0,1]单调递增,
∴1=h(0)<h(x)≤h(1)=e2-1.
∴g′(x)<0,∴g(x)在x∈(0,1]单调递减.
∴c≥g(1)=-
| 1 |
| e2 |
②当x≥1时,令v(x)=lnx-
| x |
| e2x |
| x |
| e2x |
则m′(x)=
| 1 |
| x |
| 1-2x |
| e2x |
| e2x+x(2x-1) |
| xe2x |
故m(x)在[1,+∞)上单调递增,∴c≥m(1)=-
| 1 |
| e2 |
综上①②可知:当c<-
| 1 |
| e2 |
当c=-
| 1 |
| e2 |
当c>-
| 1 |
| e2 |
点评:本题综合考查了利用导数研究函数的单调性、极值最值、数形结合的思想方法、分类讨论的思想方法等基础知识与基本技能,考查了推理能力和计算能力及其化归思想方法.

练习册系列答案
相关题目