Question

已知A(x₁,y₁),B(x₂,y₂)是函数f(x)=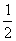的图象上的任意两点(可以重合),点M在直线x=上,且=.

(1)求x₁+x₂的值及y₁+y₂的值;

(2)已知S₁=0,当n≥2时,S_n=f()+f()+f()+…+f(),求S_n;

(3)在(2)的条件下,设a_n=2^S_n,T_n为数列{a_n}的前n项和,若存在正整数c、m,使得不等式＜成立,求c和m的值.

Answer 1

解:(1)∵点M在直线x=上,设M(,y_m).

又=,即=(-x₁,y_m-y₁),=(x₂,y₂-y_m),∴x₁+x₂=1.

①当x₁=时,x₂=,y₁+y₂=f(x₁)+f(x₂)=-1-1=-2;

②当x₁≠时,x₂≠,y₁+y₂=+

====-2;

综合①②,得y₁+y₂=-2.

(2)由(1)知,当x₁+x₂=1时,y₁+y₂=-2.

∴f()+f()=-2,k=1,2,3,…,n-1.

n≥2时,S_n=f()+f()+f()+…+f().①

S_n=f()+f()+f()+…+f(),②

①+②,得2S_n=-2(n-1),则S_n=1-n.

n=1时,S₁=0满足S_n=1-n.∴S_n=1-n.

(3)a_n==2^1-n,T_n=1++…+()^n-1=2.

＜＜0＜0.T_m+1=2,2T_m-T_m+1=4-2+=2.

∴≤2＜c＜2＜2,c、m为正整数.

∴c=1.当c=1时,∴1＜2^m＜3.

∴m=1.