题目内容
已知函数
，
在
上的减函数.
（Ⅰ）求曲线
在点（1, f（1））处的切线方程；
（Ⅱ）若
在
上恒成立，求
的取值范围；
（III）关于
的方程
(
)有两个根（无理数
），求m的范围
.
解：（Ⅰ）∵,∴
,。。。。。。。。。。。1分
∴
,。。。。。。。。。。。2分
∴在点（1, f（1））处的切线方程为
，即
；。。。。。。。。。。。 3分
（Ⅱ）∵
，∴
,
在上单调递减，∴
在上恒成立，。。。。。。。。。。。 4分
∴
在上恒成立， 
。。。。。。。。。。。5分
在上单调递减，∴
∵在上恒成立，∴只需
恒成立，。。。。。。。。。。。 6分
∴
，∵
，∴
，∴
；。。。。。。。。。。。 7分
（III）由（Ⅰ）知
方程为
，
设
,则方程根的个数即为函数
的图象与x轴交点个数，。。。。。。。。。。。 8分
∵
,。。。。。。。。。。。9分
当
时，
在
上为增函数，当
时，
在
和
上为减函数，
在
上为增函数, 在
上为减函数，
在
的最大值为
，。。。。。。。。。。。 10分
又
，
，方程有两根满足：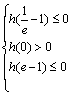
，。。。。。 11分
即
时，原方程有两解。。。。。。。。。。。 12分
练习册系列答案
相关题目