题目内容
 三棱柱ABC-A1B1C1中,M、N分别是A1B、B1C1上的点,且BM=2A1M,C1N=2B1N.设
三棱柱ABC-A1B1C1中,M、N分别是A1B、B1C1上的点,且BM=2A1M,C1N=2B1N.设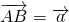 ,
, ,
, .
.
(Ⅰ)试用 表示向量
表示向量 ;
;
(Ⅱ)若∠BAC=90°,∠BAA1=∠CAA1=60°,AB=AC=AA1=1,求MN的长..
解:(Ⅰ)由图形知 =
= =
= .
.
(Ⅱ)由题设条件
∵ =
= ,
,
∴ ,
, .
.
分析:(Ⅰ)由图形知 =
= 再用
再用 表示出来即可
表示出来即可
(Ⅱ)求MN的长,即求 ,利用求向量模的方法,求
,利用求向量模的方法,求 即可求得MN的长
即可求得MN的长
点评:本题考查空间向量的夹角与距离求解公式,解题的关键是掌握住向量加法法则与用空间向量求线段长度的公式,空间向量法求立体几何中距离是空间向量的一个非常重要的运用.理解并记忆熟练公式是解题的知识保证.
 =
= =
= .
.(Ⅱ)由题设条件
∵
 =
= ,
,∴
 ,
, .
.分析:(Ⅰ)由图形知
 =
= 再用
再用 表示出来即可
表示出来即可(Ⅱ)求MN的长,即求
 ,利用求向量模的方法,求
,利用求向量模的方法,求 即可求得MN的长
即可求得MN的长点评:本题考查空间向量的夹角与距离求解公式,解题的关键是掌握住向量加法法则与用空间向量求线段长度的公式,空间向量法求立体几何中距离是空间向量的一个非常重要的运用.理解并记忆熟练公式是解题的知识保证.

练习册系列答案
相关题目
 在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
在三棱柱ABC-A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=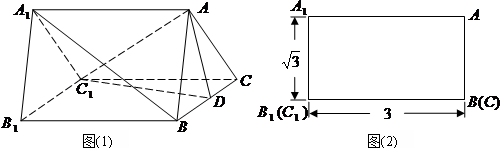
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1, 如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.
如图:在直三棱柱ABC-A1B1C1中,已知AB=A1A,AC=BC,点D、E分别为C1C、AB的中点,O为A1B与AB1的交点.