题目内容
已知函数![]() .
.
(Ⅰ)求![]() 的最小值;
的最小值;
(Ⅱ)若对所有![]() 都有
都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() 取得最小值
取得最小值![]() .(2)
.(2)![]() 的取值范围是
的取值范围是![]() .
.
解析:
先求极值再求端点值,比较求出最大(小)值.当区间只有一个极大(小)值时,该值就是最大(小)值
![]() 的定义域为
的定义域为![]() , …………1分
, …………1分
![]() 的导数
的导数![]() . ………………3分
. ………………3分
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() .
.
从而![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增. ………………5分
单调递增. ………………5分
所以,当![]() 时,
时,![]() 取得最小值
取得最小值![]() . ………………………… 6分
. ………………………… 6分
(Ⅱ)解法一:令![]() ,则
,则![]() , ……………………8分
, ……………………8分
① 若![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上为增函数,
上为增函数,
所以,![]() 时,
时,![]() ,即
,即![]() .…………………… 10分
.…………………… 10分
② 若![]() ,方程
,方程![]() 的根为
的根为 ![]() ,
,
此时,若![]() ,则
,则![]() ,故
,故![]() 在该区间为减函数.
在该区间为减函数.
所以![]() 时,
时,![]() ,
,
即![]() ,与题设
,与题设![]() 相矛盾. ……………………13分
相矛盾. ……………………13分
综上,满足条件的![]() 的取值范围是
的取值范围是![]() . ……………………………………14分
. ……………………………………14分
解法二:依题意,得![]() 在
在![]() 上恒成立,
上恒成立,
即不等式![]() 对于
对于![]() 恒成立 . ……………………8分
恒成立 . ……………………8分
令![]() , 则
, 则![]() . ……………………10分
. ……………………10分
当![]() 时,因为
时,因为![]() ,
,
故![]() 是
是![]() 上的增函数, 所以
上的增函数, 所以 ![]() 的最小值是
的最小值是![]() , ……………… 13分
, ……………… 13分
所以![]() 的取值范围是
的取值范围是![]() . …………………………………………14分
. …………………………………………14分

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.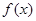 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求