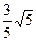题目内容
一动圆P与两圆O1：x2+y2=1和O2：x2+y2-8x+7=0均内切，那么动圆P圆心的轨迹是（ ）
| A．椭圆 | B．抛物线 |
| C．双曲线 | D．双曲线的一支 |
由圆O1：x2+y2=1得圆心O1（0，0），半径r=1；
圆O2：x2+y2-8x+7=0即（x-4）2+y2=9得圆心O2（4，0），半径R=3．
因为动圆P与两圆均内切，所以有r+|PO1|=R+|PO2|，
∴|PO1|-|PO2|=2＜|O1O2|=4，
故动圆P圆心的轨迹是双曲线的一支．
故选D．
圆O2：x2+y2-8x+7=0即（x-4）2+y2=9得圆心O2（4，0），半径R=3．
因为动圆P与两圆均内切，所以有r+|PO1|=R+|PO2|，
∴|PO1|-|PO2|=2＜|O1O2|=4，
故动圆P圆心的轨迹是双曲线的一支．
故选D．
练习册系列答案
相关题目
与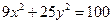
的焦距相等，则
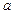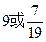
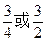
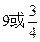
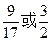
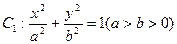的值为（ ）
的离心率为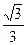
，直线l：y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切．（1）求椭圆C1的方程；（2）设椭圆C1的左焦点为F1，右焦点为F2，直线l1过点F1，且垂直于椭圆的长轴，动直线l2垂直于l1，垂足为点P，线段PF2的垂直平分线交l2于点M，求点M的轨迹C2的方程；（3）过椭圆C1的左顶点A做直线m，与圆O相交于两点R、S，若
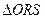是钝角三角形，求直线m的斜率k的取值范围．
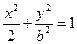的焦点为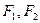
,两条准线与x轴的交点分别为M、N，若
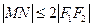，则该椭圆离心率取得最小值时的椭圆方程为 ( )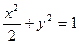
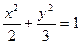
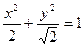
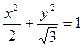
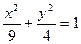，椭圆左焦点为
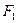，O为坐标原点，A是椭圆上一点，点M在线段
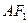上且，
，则点A的横坐标为（ ）
