题目内容
已知数列 满足:
满足:
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)令 (
( ),如果对任意
),如果对任意 ,都有
,都有 ,
,
求实数 的取值范围.
的取值范围.
【答案】
Ⅰ)由题可知: ①
①
 ②
②
②-①可得 ……………………..3分
……………………..3分
即: ,又
,又 …………………………………..5分
…………………………………..5分
所以数列 是以
是以 为首项,以
为首项,以 为公比的等比数列………………….…..6分
为公比的等比数列………………….…..6分
(Ⅱ)由(2)可得 ,
……………………………...7分
,
……………………………...7分
 ………………………...8分
………………………...8分
由 可得
可得
由 可得
可得 …………………………………....9分
…………………………………....9分
所以  故
故 有最大值
有最大值
所以,对任意 ,有
,有 ………………………………………....11分
………………………………………....11分
如果对任意 ,都有
,都有 ,即
,即 成立,
成立,
则 ,故有:
,故有: , ………………………………………....13分
, ………………………………………....13分
解得 或
或 所以,实数
所以,实数 的取值范围是
的取值范围是
【解析】(Ⅰ) ,递写相减得
,递写相减得
 ;(Ⅱ)由
;(Ⅱ)由 求出
求出 ,利用
,利用 判断数列的单调性,根据
判断数列的单调性,根据 求范围。
求范围。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于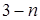 B.
B. C.
C.  D.
D. 
 满足:
满足: .
. ;
; ,求数列
,求数列 的通项公式;
的通项公式; ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.