题目内容
已知数列 满足:
满足: .
.
(Ⅰ)求 ;
;
(Ⅱ)设 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ) 
∵ ∴
∴ ……3分
……3分
(Ⅱ)∵ ∴
∴
∴数列{ }是以-4为首项,-1为公差的等差数列.∴
}是以-4为首项,-1为公差的等差数列.∴ . --------6分
. --------6分
(Ⅲ)由于 ,所以
,所以 ,从而
,从而 --------7分
--------7分
∴
∴ --------8分
--------8分
由条件可知 恒成立即可满足条件,设
恒成立即可满足条件,设
当 时,
时, 恒成立
恒成立
当 时,由二次函数的性质知不可能成立
时,由二次函数的性质知不可能成立
当 时,对称轴
时,对称轴
 ,
, 在
在 为单调递减函数.
为单调递减函数.
 ,∴
,∴ ∴
∴ 时
时 恒成立。综上知:
恒成立。综上知: 时,
时, 恒成立
恒成立
【解析】略

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
 满足
满足 ,则此数列的通项
,则此数列的通项 等于
等于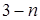 B.
B. C.
C.  D.
D. 