题目内容
6.已知符号函数sgnx=$\left\{\begin{array}{l}{1,}&{x>0}\\{0,}&{x=0}\\{-1,}&{x<0}\end{array}\right.$,f(x)是R上的增函数,g(x)=f(x)-f(ax)(a>1),则( )| A. | sgn[g(x)]=sgnx | B. | sgn[g(x)]=-sgnx | C. | sgn[g(x)]=sgn[f(x)] | D. | sgn[g(x)]=-sgn[f(x)] |
分析 直接利用特殊法,设出函数f(x),以及a的值,判断选项即可.
解答 解:由于本题是选择题,可以采用特殊法,符号函数sgnx=$\left\{\begin{array}{l}{1,}&{x>0}\\{0,}&{x=0}\\{-1,}&{x<0}\end{array}\right.$,f(x)是R上的增函数,g(x)=f(x)-f(ax)(a>1),
不妨令f(x)=x,a=2,
则g(x)=f(x)-f(ax)=-x,
sgn[g(x)]=-sgnx.所以A不正确,B正确,
sgn[f(x)]=sgnx,C不正确;D正确;
对于D,令f(x)=x+1,a=2,
则g(x)=f(x)-f(ax)=-x,
sgn[f(x)]=sgn(x+1)=$\left\{\begin{array}{l}1,&x>-1\\ 0,&x=-1\\-1,&x<-1\end{array}\right.$;
sgn[g(x)]=sgn(-x)=$\left\{\begin{array}{l}1,&x>0\\ 0,&x=0\\-1,&x<0\end{array}\right.$,
-sgn[f(x)]=-sgn(x+1)=$\left\{\begin{array}{l}-1,&x>-1\\ 0,&x=-1\\ 1,&x<-1\end{array}\right.$;所以D不正确;
故选:B.
点评 本题考查函数表达式的比较,选取特殊值法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
16.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )
| A. | 抽签法 | B. | 系统抽样法 | C. | 分层抽样法 | D. | 随机数法 |
18.阅读如图所示的程序框图,运行相应的程序,则输出i的值为( )
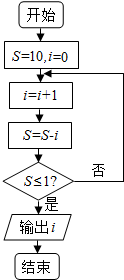

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
15.设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β,( )
| A. | 若l⊥β,则α⊥β | B. | 若α⊥β,则l⊥m | C. | 若l∥β,则α∥β | D. | 若α∥β,则l∥m |
 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,
如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1,