题目内容
(本小题满分12分)
已知函数 ,
,  .
.
(Ⅰ)求函数 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设函数 在
在 上的图象与
上的图象与 轴的交点从左到右分别为M,N,图象的最高点为P, 求向量
轴的交点从左到右分别为M,N,图象的最高点为P, 求向量 与
与 夹角的余弦值.
夹角的余弦值.
已知函数
 ,
,  .
.(Ⅰ)求函数
 的最大值和最小值;
的最大值和最小值;(Ⅱ)设函数
 在
在 上的图象与
上的图象与 轴的交点从左到右分别为M,N,图象的最高点为P, 求向量
轴的交点从左到右分别为M,N,图象的最高点为P, 求向量 与
与 夹角的余弦值.
夹角的余弦值.解:(Ⅰ)∵ =
=
= ----------------------4分
----------------------4分
∵ ∴
∴ ,
,
∴函数 的最大值和最小值分别为2,-2.---------------6分
的最大值和最小值分别为2,-2.---------------6分
(Ⅱ)解法1:令 得
得 ,
,
∵ ∴
∴ 或
或 ∴
∴ --------8分
--------8分
由 ,且
,且 得
得 ∴
∴ -------------9分
-------------9分
∴ ,
, ,从而
,从而
∴
 .------------------------12分
.------------------------12分
解法2:过点P作 轴于
轴于 ,则
,则 ,由三角函数的性质知
,由三角函数的性质知 -8分
-8分
 ,-------------------------9分
,-------------------------9分
由余弦定理得 =
= .--12分
.--12分
解法3:过点P作 轴于
轴于 ,则
,则 由三角函数的性质知
由三角函数的性质知 ,-8分
,-8分
 --------------------------9分
--------------------------9分
在 中,
中, --------11分
--------11分
∵PA平分 ∴
∴
 .----------------------------------12分
.----------------------------------12分
 =
=
=
 ----------------------4分
----------------------4分∵
 ∴
∴ ,
,∴函数
 的最大值和最小值分别为2,-2.---------------6分
的最大值和最小值分别为2,-2.---------------6分(Ⅱ)解法1:令
 得
得 ,
,∵
 ∴
∴ 或
或 ∴
∴ --------8分
--------8分由
 ,且
,且 得
得 ∴
∴ -------------9分
-------------9分∴
 ,
, ,从而
,从而∴

 .------------------------12分
.------------------------12分解法2:过点P作
 轴于
轴于 ,则
,则 ,由三角函数的性质知
,由三角函数的性质知 -8分
-8分 ,-------------------------9分
,-------------------------9分由余弦定理得
 =
= .--12分
.--12分解法3:过点P作
 轴于
轴于 ,则
,则 由三角函数的性质知
由三角函数的性质知 ,-8分
,-8分 --------------------------9分
--------------------------9分在
 中,
中, --------11分
--------11分∵PA平分
 ∴
∴
 .----------------------------------12分
.----------------------------------12分略

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 的图象向左平移
的图象向左平移 个单位, 再向上平移1个单位,所得图象的函
个单位, 再向上平移1个单位,所得图象的函



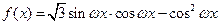
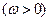 最小正周期为
最小正周期为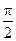 .
.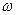 的值及函数
的值及函数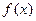 的解析式;
的解析式;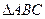 的三条边
的三条边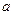 ,
,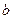 ,
,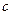 满足
满足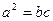 ,
,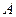 .求角
.求角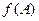 的值域.
的值域. ,其中
,其中 .若
.若 满足
满足 ,且
,且 的导函数
的导函数 的图象关于直线
的图象关于直线 对称.
对称. 的值;
的值; 的方程
的方程 在区间
在区间 上总有实数解,求实数
上总有实数解,求实数 的取值范围.
的取值范围.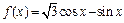 的图象向右平移
的图象向右平移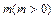 个单位长度后,所得图象对应的函
个单位长度后,所得图象对应的函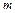 的最小值是
的最小值是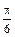
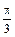
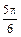
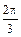
 ,从B处望A的府角是β则,α,β之间的关系是 ( )
,从B处望A的府角是β则,α,β之间的关系是 ( ) bc,求:
bc,求: 在
在 上的最值
上的最值 