题目内容
已知向量m=(1+cosB,sinB)与向量n=(0,1)所成的角为(1)求角B的大小;
(2)若AC=![]() ,求△ABC周长的最大值.
,求△ABC周长的最大值.
答案:解法一:(1)∵m=(1+cosB,sinB)与n=(0,1)所成的角为![]()
∴m与向量p=(1,0)所成的角为![]()
∴![]() ,即tan
,即tan![]()
而B∈(0,π),∴![]() ∈(0,
∈(0,![]() ),∴
),∴![]() ,∴B=
,∴B=![]() .
.
(2)令AB=c,BC=a,AC=b
∵B=![]() ,∴b2=a2+c2-2accosB=a2+c2-ac=(
,∴b2=a2+c2-2accosB=a2+c2-ac=(![]() )2,∵a,c>0.
)2,∵a,c>0.
∴a2+c2≥![]() ,ac≤(
,ac≤(![]() )2(当且仅当n=c时等号成立)
)2(当且仅当n=c时等号成立)
∴12=a2+c2-ac≥![]()
∴(a+c)2≤48,∴a+c≤![]() ,
,
∴a+b+c≤![]() (当且仅当a=c时取等号)
(当且仅当a=c时取等号)
故△ABC的周长的最大值为![]() .
.
解法二:(1)cos<m,n>=cos![]()
∴![]() ,即2cos2B+cosB-1=0,cosB=
,即2cos2B+cosB-1=0,cosB=![]() 或cosB=-1(舍)
或cosB=-1(舍)
而B∈(0,π),∴B=![]() .
.
(2)令AB=c,BC=a,AC=b,△ABC的周长为l,则l=a+c+![]()
而a=b·![]() ,c=b·
,c=b·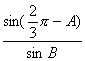
=![]()
=![]()
![]()
=![]()
∵A∈(0,![]() ),∴A
),∴A![]() (
(![]() )
)
当且仅当A=![]() 时,lmax=
时,lmax=![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知向量
=(1,1),
=(1,a),其中a为实数,当
与
的夹角在区间(0,
)范围内变动时,实数a的取值范围是( )
. |
| m |
. |
| n |
. |
| m |
. |
| n |
| π |
| 12 |
| A、(0,1) | ||||||
B、(
| ||||||
C、(
| ||||||
D、(1,
|