题目内容
已知函数![]() 且
且![]()
(1)若![]() 在
在![]() 取得极小值-2,求函数
取得极小值-2,求函数![]() 的单调区间
的单调区间
(2)令![]() 若
若![]() 的解集为A,且
的解集为A,且![]() ,求
,求![]() 的范围
的范围
(1)![]() 的单调递减区间是[-1,1], 单调递增区间是(-∞,1
的单调递减区间是[-1,1], 单调递增区间是(-∞,1![]() 和
和![]()
(2)由A![]() 知
知![]() 。解得
。解得![]()
解析:
(I)∵![]() ,且
,且![]() ,
,
∴![]() ①④
①④
又由在![]() 处取得极小值-2可知
处取得极小值-2可知![]() ②且
②且![]() ③
③
将①②③式联立得![]() ∴
∴![]() 。
。![]() (4分)
(4分)
由![]() 得
得![]() 同理由
同理由![]() 得
得![]()
∴![]() 的单调递减区间是[-1,1], 单调递增区间是(-∞,1
的单调递减区间是[-1,1], 单调递增区间是(-∞,1![]() 和
和![]() (6分)
(6分)
(II)由上问知:![]() ,∴
,∴![]() 。
。
又∵![]() 。∴
。∴![]() 。∴
。∴![]() 。∴
。∴![]()
∵![]() ,∴
,∴![]() >0。∴
>0。∴![]() 。(8分)
。(8分)
∴当![]() 时,
时,![]() 的解集是
的解集是![]() ,
,
显然A![]() 不成立,不满足题意。
不成立,不满足题意。
∴![]() ,且
,且![]() 的解集是
的解集是![]() 。 (10分)
。 (10分)
又由A![]() 知
知![]() 。解得
。解得![]() 。(12分)
。(12分)

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 且
且 (1)求
(1)求 的单调区间;
的单调区间; 与函数
与函数 时有相同的值域,求
时有相同的值域,求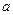 的值;
的值; ,函数
,函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得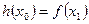 成立,求
成立,求 且
且
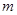 的值;(2)判定
的值;(2)判定 的奇偶性;
的奇偶性;