题目内容
已知函数f(x)=x3-(k2-k+1)x2+5x-2,g(x)=k2x2+kx+1,其中x∈R。
(1)设函数p(x)=f(x)+g(x)。若p(x)在区间(0,3)上不单调,求k的取值范围;
(2)设函数 ,否存在k,对任意给定的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得q'(x2)=q'(x1)成立?若存在,求k的值;若不存在,请说明理由。
,否存在k,对任意给定的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得q'(x2)=q'(x1)成立?若存在,求k的值;若不存在,请说明理由。
(1)设函数p(x)=f(x)+g(x)。若p(x)在区间(0,3)上不单调,求k的取值范围;
(2)设函数
 ,否存在k,对任意给定的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得q'(x2)=q'(x1)成立?若存在,求k的值;若不存在,请说明理由。
,否存在k,对任意给定的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得q'(x2)=q'(x1)成立?若存在,求k的值;若不存在,请说明理由。解:(1)p(x)=f(x)+g(x)=x3+(k-1)x2+(k+5)x-1,
P '(x)=3x2+2(k-1)x+(k+5)
因为p(x)在(0,3)上不单调,
所以p'(x)=0在(0,3)上有实数解,且无重根,
由p'(x)=0,得k(2x+1)=-(3x2-2x+5)
即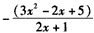
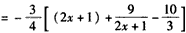
令t=2x+1,有t∈(1,7),记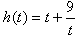
则h(t)在(1,3]上单调递减,在[3,7)上单调递增,
所以,h(t)∈[6,10)
于是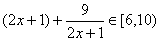
得k∈(-5,-2]
而当k=-2时,p'(x)=0在(0,3)上有两个相等的实根x=1,
故舍去,所以k∈(-5,-2)。
(2)由题意,得当x<0时,
q'(x)=f'(x)=3x2-2(k2-k+1)x+5
当x>0时,g'(x)=g'(x)=2k2x+k.
因为当k=0时不合题意,所以k≠0
下面讨论k≠0的情形
记A={g'(x)|x>0},B={f'(x)|x<0}
则A=(k,+∞),B=(5,+∞)
(i)当x1>0时,q'(x)在(0,+∞)上单调递增,
所以要使q'(x2)=q'(x1)成立,只能x2<0,且A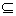 B,因此k≥5;
B,因此k≥5;
(ii)当x1<0时,q'(x)在(-∞,0)上单调递减,
所以要使q'(x2)=q'(x1)成立,只能x2>0,且B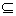 A,因此k≤5
A,因此k≤5
综合(i)(ii),得k=5。
当k=5时,有A=B
则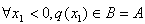
即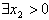 ,使得q'(x2)=q'(x1)成立
,使得q'(x2)=q'(x1)成立
因为q'(x)在(0,+∞)上单调递增,所以x2是唯一的。
同理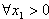 ,存在唯一的非零实数x2(x2≠x1),使得q'(x2) =q'(x1)成立
,存在唯一的非零实数x2(x2≠x1),使得q'(x2) =q'(x1)成立
所以k=5满足题意。
P '(x)=3x2+2(k-1)x+(k+5)
因为p(x)在(0,3)上不单调,
所以p'(x)=0在(0,3)上有实数解,且无重根,
由p'(x)=0,得k(2x+1)=-(3x2-2x+5)
即
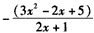
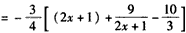
令t=2x+1,有t∈(1,7),记
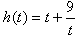
则h(t)在(1,3]上单调递减,在[3,7)上单调递增,
所以,h(t)∈[6,10)
于是
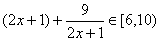
得k∈(-5,-2]
而当k=-2时,p'(x)=0在(0,3)上有两个相等的实根x=1,
故舍去,所以k∈(-5,-2)。
(2)由题意,得当x<0时,
q'(x)=f'(x)=3x2-2(k2-k+1)x+5
当x>0时,g'(x)=g'(x)=2k2x+k.
因为当k=0时不合题意,所以k≠0
下面讨论k≠0的情形
记A={g'(x)|x>0},B={f'(x)|x<0}
则A=(k,+∞),B=(5,+∞)
(i)当x1>0时,q'(x)在(0,+∞)上单调递增,
所以要使q'(x2)=q'(x1)成立,只能x2<0,且A
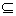 B,因此k≥5;
B,因此k≥5;(ii)当x1<0时,q'(x)在(-∞,0)上单调递减,
所以要使q'(x2)=q'(x1)成立,只能x2>0,且B
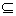 A,因此k≤5
A,因此k≤5综合(i)(ii),得k=5。
当k=5时,有A=B
则
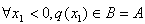
即
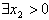 ,使得q'(x2)=q'(x1)成立
,使得q'(x2)=q'(x1)成立因为q'(x)在(0,+∞)上单调递增,所以x2是唯一的。
同理
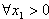 ,存在唯一的非零实数x2(x2≠x1),使得q'(x2) =q'(x1)成立
,存在唯一的非零实数x2(x2≠x1),使得q'(x2) =q'(x1)成立所以k=5满足题意。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|