题目内容
抛物线y2=4x的焦点为F,准线l与x轴相交于点E,过F且倾斜角等于60°的直线与抛物线在x轴上方的部分相交于点A,AB⊥l,垂足为B,则四边形ABEF的面积等于( )A.
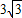
B.
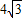
C.
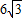
D.
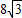
【答案】分析:先判断△ABF为等边三角形,求出A的坐标,而四边形ABEF为直角梯形,可求出直角梯形的上底边长AB=m+1的值,直角梯形的面积可求.
解答:解:由抛物线的定义可得AF=AB,∵AF的倾斜角等于60°,
∵AB⊥l,∴∠FAB=60°,故△ABF为等边三角形.
又焦点F(1,0),AF的方程为 y-0=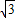 (x-1),
(x-1),
设A(m,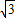 m-
m-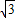 ),m>1,由AF=AB,得
),m>1,由AF=AB,得 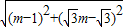 =m+1,
=m+1,
∴m=3,故等边三角形△ABF的边长AB=m+1=4,
△ABF为等边三角形,
∴四边形ABEF的面积是 (EF+AB)BE=
(EF+AB)BE= (2+4)×4sin60°=6
(2+4)×4sin60°=6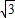 ,
,
故选C.
点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,判断四边形ABEF为直角梯形是解题的关键.
解答:解:由抛物线的定义可得AF=AB,∵AF的倾斜角等于60°,
∵AB⊥l,∴∠FAB=60°,故△ABF为等边三角形.
又焦点F(1,0),AF的方程为 y-0=
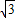 (x-1),
(x-1),设A(m,
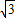 m-
m-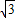 ),m>1,由AF=AB,得
),m>1,由AF=AB,得 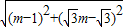 =m+1,
=m+1,∴m=3,故等边三角形△ABF的边长AB=m+1=4,
△ABF为等边三角形,
∴四边形ABEF的面积是
 (EF+AB)BE=
(EF+AB)BE= (2+4)×4sin60°=6
(2+4)×4sin60°=6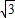 ,
,故选C.
点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,判断四边形ABEF为直角梯形是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目