题目内容
(1)在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于- .求动点P的轨迹方程.
.求动点P的轨迹方程.
(2) 的离心率为2,原点到直线AB的距离为
的离心率为2,原点到直线AB的距离为 ,其中A(0,-b)、B(a,0)求该双曲线的标准方程.
,其中A(0,-b)、B(a,0)求该双曲线的标准方程.
解:(1)∵点B与点A(-1,1)关于原点O对称,∴B(1,-1),
设点P的坐标为(x,y),则
∵直线AP与BP的斜率之积等于- ,
,
∴ •
• =-
=-
化简可得x2+3y2=4(x≠±1);
(2)∵e=2,∴ ,∴b2=3a2①
,∴b2=3a2①
∵AB的方程为bx-ay-ab=0
∴由点到直线的距离公式可得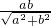 =
= ②
②
联立①②,解得a2=1,b2=3
∴双曲线方程为 .
.
分析:(1)求出B的坐标,利用直线AP与BP的斜率之积等于- ,即可得到动点P的轨迹方程;
,即可得到动点P的轨迹方程;
(2)利用离心率为2,原点到直线AB的距离为 ,建立方程,即可求得轨迹方程.
,建立方程,即可求得轨迹方程.
点评:本题考查轨迹方程,考查学生的计算能力,属于中档题.
设点P的坐标为(x,y),则
∵直线AP与BP的斜率之积等于-
 ,
,∴
 •
• =-
=-
化简可得x2+3y2=4(x≠±1);
(2)∵e=2,∴
 ,∴b2=3a2①
,∴b2=3a2①∵AB的方程为bx-ay-ab=0
∴由点到直线的距离公式可得
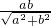 =
= ②
②联立①②,解得a2=1,b2=3
∴双曲线方程为
 .
.分析:(1)求出B的坐标,利用直线AP与BP的斜率之积等于-
 ,即可得到动点P的轨迹方程;
,即可得到动点P的轨迹方程;(2)利用离心率为2,原点到直线AB的距离为
 ,建立方程,即可求得轨迹方程.
,建立方程,即可求得轨迹方程.点评:本题考查轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目