题目内容
已知函数y=lg(x2+2x+a)
(1)若函数定义域为R,求a的取值范围;
(2)若函数的值域为[0,+∞),求a的取值范围.
(1)若函数定义域为R,求a的取值范围;
(2)若函数的值域为[0,+∞),求a的取值范围.
分析:(1)给出的函数是对数型的复合函数,函数的定义域为实数集,说明取任意实数都有真数大于0,然后结合“三个二次”求解;
(2)对数型复合函数的外层函数时增函数,要使函数的值域为[0,+∞),只需要内层函数的值域是[1,+∞),然后求解使内层二次函数的最小值为1的a值.
(2)对数型复合函数的外层函数时增函数,要使函数的值域为[0,+∞),只需要内层函数的值域是[1,+∞),然后求解使内层二次函数的最小值为1的a值.
解答:解:(1)函数y=lg(x2+2x+a)的定义域为R,说明对任意x∈R,x2+2x+a>0恒成立,
因为二次函数y=x2+2x+a的图象开口向上,所以只需22-4a<0即可,所以a>1;
(2)令g(x)=x2+2x+a,函数y=lg(x2+2x+a)的值域为[0,+∞),
即函数g(x)=x2+2x+a的值域是[1,+∞),由
=1,得:a=2.
所以使函数y=lg(x2+2x+a)的值域为[0,+∞)的a的取值范围是{2}.
因为二次函数y=x2+2x+a的图象开口向上,所以只需22-4a<0即可,所以a>1;
(2)令g(x)=x2+2x+a,函数y=lg(x2+2x+a)的值域为[0,+∞),
即函数g(x)=x2+2x+a的值域是[1,+∞),由
| 4a-22 |
| 4 |
所以使函数y=lg(x2+2x+a)的值域为[0,+∞)的a的取值范围是{2}.
点评:本题考查了函数的定义域及其求法,考查了逆向思维方式,训练了利用“三个二次”结合求解不等式,此题是基础题,但容易出错.

练习册系列答案
相关题目
已知函数y=lg(x+a)的图象如图所示,则a的值为( )
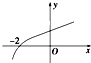

| A、2 | B、3 | C、4 | D、5 |