题目内容
(本小题共12分)已知函数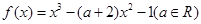 ,
,
⑴若函数f(x)在区间(0,2)上递减,在[2,+∞)上递增,求a的值;
⑵在①的条件下是否存在实数m,使得函数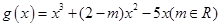 的图像与函数
的图像与函数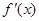 的图像恰好有三个不同的交点,若存在,请求出实数m的取值范
的图像恰好有三个不同的交点,若存在,请求出实数m的取值范 围;若不存在,请说明理由。
围;若不存在,请说明理由。
【答案】
⑴
⑵m∈(-∞,-3) ∪(1,+∞)理由略
【解析】解:⑴ (2分)
(2分)
∵函数f(x)在区间(0 ,2)上递减,在[2,+∞)上递增,所以一定有
,2)上递减,在[2,+∞)上递增,所以一定有
即 (4分)
(4分)
⑵由⑴知a=1,
故此时 的图像与函数
的图像与函数 的图像恰好有三个不同的交点。
的图像恰好有三个不同的交点。
即方程
化简为 有三个不同的实根 (8分)
有三个不同的实根 (8分)
即x[x2-(m+1)x+1]=0
解得x=0或x2-(m+1)x+1=0
 (10分)
(10分)
∴ 方程x2-(1+m)x+1=0必有两个非零相异实根,
∴△=(1+m)2-4>0
∴m>1或m<-3
即m∈(-∞,-3) ∪(1,+∞) (12分)

练习册系列答案
相关题目
 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间; 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(- ,0)和F2(
,0)和F2( 与曲线
与曲线 为坐标原点),求直线
为坐标原点),求直线
 的最小正周期和最小值;
的最小正周期和最小值; ,
, ,求证:
,求证: .
.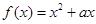 的最小值不小于
的最小值不小于 , 且
, 且 .
. 的解析式;
的解析式; 的最小值为实数
的最小值为实数 的函数
的函数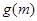 ,求函数
,求函数 ,集合
,集合
 ,求实数
,求实数 的取值范围.
的取值范围.