题目内容
(本小题共12分)已知曲线 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(- ,0)和F2(
,0)和F2( ,0)的距离之和为4.
,0)的距离之和为4.
(1)求曲线 的方程;
的方程;
(2)设过(0,-2)的直线 与曲线
与曲线 交于C、D两点,且
交于C、D两点,且 为坐标原点),求直线
为坐标原点),求直线 的方程.
的方程.
【答案】
解:(1)根据椭圆的定义,可知动点 的轨迹为椭圆, ……………………1分
的轨迹为椭圆, ……………………1分
其中 ,
, ,则
,则 . ……………………………2分
. ……………………………2分
所以动点M的轨迹方程为 .……………………………………4分
.……………………………………4分
(2)当直线 的斜率不存在时,不满足题意.………………………………5分
的斜率不存在时,不满足题意.………………………………5分
当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 ,设
,设 ,
, ,∵
,∵ ,∴
,∴ .………………6分
.………………6分
∵ ,
, ,
,
∴ .
.
∴  .………… ① ……………7分
.………… ① ……………7分
由方程组 得
得 .
.
则 ,
, ,………………………………9分
,………………………………9分
代入①,得 .
.
即 ,解得,
,解得, 或
或 .…………………………………11分
.…………………………………11分
所以,直线 的方程是
的方程是 或
或 .…………………12分
.…………………12分
【解析】略

练习册系列答案
相关题目
 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
 的最小正周期和最小值;
的最小正周期和最小值; ,
, ,求证:
,求证: .
.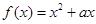 的最小值不小于
的最小值不小于 , 且
, 且 .
. 的解析式;
的解析式; 的最小值为实数
的最小值为实数 的函数
的函数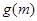 ,求函数
,求函数 ,集合
,集合
 ,求实数
,求实数 的取值范围.
的取值范围.