题目内容
已知数列{an},{bn}满足: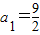 ,
,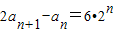 ,
,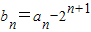 (n∈N*).
(n∈N*).(Ⅰ)证明数列{bn}为等比数列.并求数列{an},{bn}的通项公式;
(Ⅱ)记数列{an},{bn}的前n项和分别为Sn,Tn,若对任意的n∈N*都有
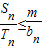 ,求实数m的最小值.
,求实数m的最小值.
【答案】分析:(Ⅰ)利用数列递推式整理变形,利用等比数列的定义,可得数列{bn}为等比数列,从而可求数列{an},{bn}的通项公式;
(Ⅱ)对任意的n∈N*都有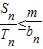 ,等价于
,等价于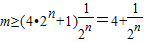 对任意的n∈N*成立,由此可求实数m的最小值.
对任意的n∈N*成立,由此可求实数m的最小值.
解答:(Ⅰ)证明:由已知得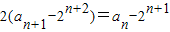 ,…(2分)
,…(2分)
∵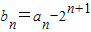 ,∴2bn+1=bn
,∴2bn+1=bn
∵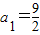 ,∴
,∴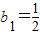 ,
,
∴{bn}为等比数列.…(4分)
所以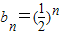 ,…(6分)
,…(6分)
进而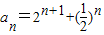 .…(7分)
.…(7分)
(Ⅱ)解: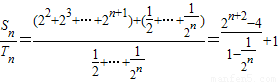 =4•2n+1…(10分)
=4•2n+1…(10分)
则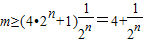 对任意的n∈N*成立. …(12分)
对任意的n∈N*成立. …(12分)
∵数列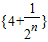 是递减数列,∴
是递减数列,∴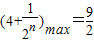
∴m的最小值为 . …(14分)
. …(14分)
点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项,考查恒成立问题,正确求通项是关键.
(Ⅱ)对任意的n∈N*都有
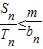 ,等价于
,等价于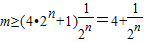 对任意的n∈N*成立,由此可求实数m的最小值.
对任意的n∈N*成立,由此可求实数m的最小值.解答:(Ⅰ)证明:由已知得
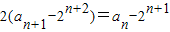 ,…(2分)
,…(2分)∵
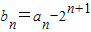 ,∴2bn+1=bn
,∴2bn+1=bn∵
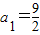 ,∴
,∴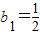 ,
,∴{bn}为等比数列.…(4分)
所以
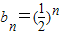 ,…(6分)
,…(6分)进而
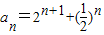 .…(7分)
.…(7分)(Ⅱ)解:
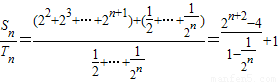 =4•2n+1…(10分)
=4•2n+1…(10分)则
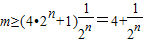 对任意的n∈N*成立. …(12分)
对任意的n∈N*成立. …(12分)∵数列
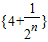 是递减数列,∴
是递减数列,∴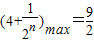
∴m的最小值为
 . …(14分)
. …(14分)点评:本题考查数列递推式,考查等比数列的证明,考查数列的通项,考查恒成立问题,正确求通项是关键.

练习册系列答案
相关题目