题目内容
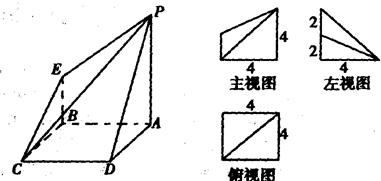
如图是一几何体的直观图、主视图、俯视图、左视图．
（1）若F为PD的中点，求证：AF⊥面PCD；
（2）证明BD∥面PEC．
（1）若F为PD的中点，求证：AF⊥面PCD；
（2）证明BD∥面PEC．
（1）由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥面ABCD，
PA∥EB，PA=2EB=4．∵PA=AD，F为PD的中点，
∴PD⊥AF，
又∵CD⊥DA，CD⊥PA，PA∩DA=A，
∴CD⊥面ADP，
∴CD⊥AF．又CD∩DP=D，∴AF⊥面PCD．
（2）取PC的中点M，AC与BD的交点为N，连接MN，
∴MN=
PA，MN∥PA，
∴MN=EB，MN∥EB，故四边形BEMN为平行四边形，
∴EM∥BN，又EM?面PEC，∴BD∥面PEC．
PA∥EB，PA=2EB=4．∵PA=AD，F为PD的中点，
∴PD⊥AF，
又∵CD⊥DA，CD⊥PA，PA∩DA=A，
∴CD⊥面ADP，
∴CD⊥AF．又CD∩DP=D，∴AF⊥面PCD．
（2）取PC的中点M，AC与BD的交点为N，连接MN，
∴MN=
| 1 |
| 2 |
∴MN=EB，MN∥EB，故四边形BEMN为平行四边形，
∴EM∥BN，又EM?面PEC，∴BD∥面PEC．
练习册系列答案
相关题目
如图是一几何体的直观图、主视图、俯视图、左视图．
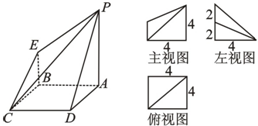如图是一几何体的直观图、主视图、俯视图、左视图．
（2012•云南模拟）如图是一几何体的直观图、主视图、俯视图、左视图．