题目内容
 (2012•云南模拟)如图是一几何体的直观图、主视图、俯视图、左视图.
(2012•云南模拟)如图是一几何体的直观图、主视图、俯视图、左视图.(1)若F为PD的中点,求证:AF⊥面PCD;
(2)求A到面PEC的距离.
分析:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,证明PD⊥AF,CD⊥AF,然后证明AF⊥面PCD.
(2)由VC-PEA=VA-PEC,直接求解A到面PEC的距离.
(2)由VC-PEA=VA-PEC,直接求解A到面PEC的距离.
解答:解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥面ABCD,
PA∥EB,PA=2EB=4.∵PA=AD,F为PD的中点,∴PD⊥AF,
又∵CD⊥DA,CD⊥PA
∴CD⊥AF,
CD∩PD=D,
∴AF⊥面PCD…(6分)
(2)由已知三视图的数据可得PA=4,AD=AB=4,BE=2,
所以 PC=PE=2
, PC=4
…(6分)
S△PCE=
•4
•2
=4
,S△PEA=
•4•4=8
由VC-PEA=VA-PEC,得
×8×4=
×h×4
;
解得,h=
=
…(12分)
PA∥EB,PA=2EB=4.∵PA=AD,F为PD的中点,∴PD⊥AF,
又∵CD⊥DA,CD⊥PA
∴CD⊥AF,
CD∩PD=D,
∴AF⊥面PCD…(6分)
(2)由已知三视图的数据可得PA=4,AD=AB=4,BE=2,
所以 PC=PE=2
| 5 |
| 3 |
S△PCE=
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
| 1 |
| 2 |

由VC-PEA=VA-PEC,得
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |
解得,h=
| 8 | ||
|
4
| ||
| 3 |
点评:本题考查直线与平面垂直的判定定理的应用,等体积法求解点到平面的距离,考查计算能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
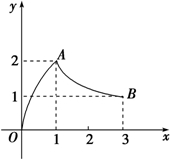 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(