题目内容
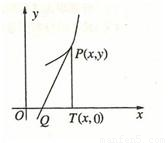
如图，曲线y=f（x）上任一点P的切线PQ交x轴于Q，过P作PT垂直于x轴于T，若△PTQ的面积为
，则y与y'的关系满足
- A.y=y′
- B.y=-y′
- C.y=y′2
- D.y2=y′
D
分析：先根据面积求出点Q的坐标，再根据导数的几何意义即利用PQ的斜率等于在点P处的导数，建立等量关系即可．
解答：
，
∴
，
，
根据导数的几何意义，
∴y2=y′．
故选D
点评：本题主要考查了导数的几何意义，以及三角形的面积公式的运用等知识，属于基础题．
分析：先根据面积求出点Q的坐标，再根据导数的几何意义即利用PQ的斜率等于在点P处的导数，建立等量关系即可．
解答：
，∴
，，根据导数的几何意义，
∴y2=y′．
故选D
点评：本题主要考查了导数的几何意义，以及三角形的面积公式的运用等知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，曲线y=f（x）上任一点P的切线PQ交x轴于Q，过P作PT垂直于x轴于T，若△PTQ的面积为| 1 |
| 2 |
| A、y=y′ |
| B、y=-y′ |
| C、y=y′2 |
| D、y2=y′ |
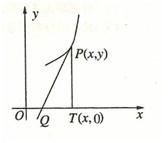
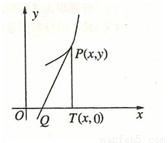
，则y与y'的关系满足（ ）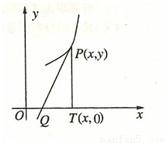
，则y与y'的关系满足（ ）
，则y与y'的关系满足（ ）