题目内容
已知函数f（x）=x2-（a+2）x+alnx，其中常数a＞0．
（1）当a＞2时，求函数f（x）的单调递增区间；
（2）当a=4时，若函数y=f（x）-m有三个不同的零点，求m的取值范围．
解：（1）由f（x）=x2-（a+2）x+alnx可知，函数的定义域为{x|x＞0}，
且
因为a＞2，所以
．
当0＜x＜1或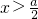
时，f'（x）＞0；当
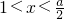时，f'（x）＜0，
所以f（x）的单调递增区间为
．
（2）当a=4时，
．
所以，当x变化时，f′（x），f（x）的变化情况如下表：
所以
，
．
函数f（x）的图象大致如下：
所以若函数y=f（x）-m有三个不同的零点，
则m∈（4ln2-8，-5）．
分析：（1）求导数f′（x），当a＞2时在函数定义域内解不等式f′（x）＞0即可．
（2）数形结合：当a=4时，用导数求出函数y=f（x）的极大值与极小值，画出草图，借助图象即可求得m的取值范围．
点评：本题考查了导数的综合应用，用导数求函数单调区间、求函数极值以及作图能力，数形结合思想在解决本题中提供了有力保障．
且
因为a＞2，所以
．当0＜x＜1或
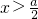时，f'（x）＞0；当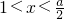时，f'（x）＜0，所以f（x）的单调递增区间为
．（2）当a=4时，
．所以，当x变化时，f′（x），f（x）的变化情况如下表：
| x | （0，1） | 1 | （1，2） | 2 | （2，+∞） |
| f′（x） | + | 0 | - | 0 | + |
| f（x） | 单调递增 | f（x）取极大值 | 单调递减 | f（x）取极小值 | 单调递增 |
，．函数f（x）的图象大致如下：
所以若函数y=f（x）-m有三个不同的零点，
则m∈（4ln2-8，-5）．
分析：（1）求导数f′（x），当a＞2时在函数定义域内解不等式f′（x）＞0即可．
（2）数形结合：当a=4时，用导数求出函数y=f（x）的极大值与极小值，画出草图，借助图象即可求得m的取值范围．
点评：本题考查了导数的综合应用，用导数求函数单调区间、求函数极值以及作图能力，数形结合思想在解决本题中提供了有力保障．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|