题目内容

（坐标系与参数方程选做题）若直线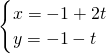数学公式（t为参数）被曲线　数学公式（θ为参数，θ∈R）所截，则截得的弦的长度是________．


分析：先求出直线的普通方程，然后根据同角三角形函数的平方关系消去θ求出圆的普通方程，然后求出圆心和半径，构造直角三角形求出弦长即可．
解答：∵直线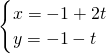（t为参数）
∴下式乘以2与上式相加可得x+2y+3=0
∵曲线 （θ为参数，θ∈R）
∴，两式平方相加得（x-1）2+（y-1）2=9
圆心为（1，1）半径为3
圆心到直线x+2y+3=0的距离为
截得的弦的长度是2×
故答案为：
点评：本题主要考查了圆的参数方程，以及直线的参数方程和弦长的度量，属于中档题．
练习册系列答案
相关题目
（坐标系与参数方程选做题）以原点为极点，x轴的正半轴为极轴，单位长度一致的坐标系下，已知曲线C1的参数方程为
x=2cosθ+3
y=2sinθ
（θ为参数），曲线C2的极坐标方程为ρsinθ=a，则这两曲线相切时实数a的值为
 
．
（坐标系与参数方程选做题）在极坐标系（ρ，θ）（ρ＞0，0≤θ＜
π
2
）中，曲线ρ=2sinθ与ρ=2cosθ的交点的极坐标为
（
2
，
π
4
）
（
2
，
π
4
）
．
（坐标系与参数方程选做题）
曲线
x=t
y=
1
3
t2
（t为参数且t＞0）与直线ρsinθ=1（ρ∈R，0≤θ＜π）交点M的极坐标为
（2，
π
6
）
（2，
π
6
）
．
（1）（坐标系与参数方程选做题）已知在极坐标系下，点A（1，
π
3
），B（3，
2π
3
），O是极点，则△AOB的面积等于
3
3
4
3
3
4
；
（2）（不等式选做题）关于x的不等式|
x+1
x-1
|＞
x+1
x-1
的解集是
（-1，1）
（-1，1）
．
（坐标系与参数方程选做题）在极坐标系中，已知点P（2，
π3
），则过点P且平行于极轴的直线的极坐标方程为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网