题目内容
设数列{an}是等差数列,a5=6,a3=2时,若自然数k1,k2,…,kn…(n∈N*)满足5<k1<k2<…<kn<…,使得a3,a5,ak1ak2,…akn,…成等比数列,
(1)求数列{an}的通项公式;
(2)求数列{kn}的通项公式及其前n项的和.
(1)求数列{an}的通项公式;
(2)求数列{kn}的通项公式及其前n项的和.
分析:(1)根据等差数列{an}的第3项和第5项求出公差d=2,再求出a1=-2,结合等差数列的通项公式即可求出an的表达式;
(2)由等比数列的通项公式,算出题中等比数列的公比q=3,从而得到第n项akn=2•3n+1,根据akn同时是{an}的第kn项建立相等关系,即可得到kn=3n+1+2,最后结合等比数列的求和公式即可得到数列{kn}的其前n项的和.
(2)由等比数列的通项公式,算出题中等比数列的公比q=3,从而得到第n项akn=2•3n+1,根据akn同时是{an}的第kn项建立相等关系,即可得到kn=3n+1+2,最后结合等比数列的求和公式即可得到数列{kn}的其前n项的和.
解答:解:(1)∵等差数列{an}中,a5=6,a3=2
∴{an}的公差d=
=
=2,可得a1=a3-2d=-2
因此,{an}的通项公式为an=a1+(n-3)×2=2n-4
(2)∵2,6,ak1,ak2,…akn,…成等比数列,
∴该数列的公比q=
=3,可得akn=2•3n+1,
又∵akn 是等差数列{an}中的第kn项,∴ak n=2kn-4,
因此,2•3n+1=2kn-4,解之得kn=3n+1+2,
∴k1+k2+…kn=(32+2)+(33+2)+(34+2)+…+(3n+1+2)
=(32+33+…3n+1)+2n=
(3n-1)+2n.
即数列{kn}的通项公式为:kn=3n+1+2,其前n项的和为
(3n-1)+2n.
∴{an}的公差d=
| a5-a3 |
| 5-3 |
| 6-2 |
| 5-3 |
因此,{an}的通项公式为an=a1+(n-3)×2=2n-4
(2)∵2,6,ak1,ak2,…akn,…成等比数列,
∴该数列的公比q=
| 6 |
| 2 |
又∵akn 是等差数列{an}中的第kn项,∴ak n=2kn-4,
因此,2•3n+1=2kn-4,解之得kn=3n+1+2,
∴k1+k2+…kn=(32+2)+(33+2)+(34+2)+…+(3n+1+2)
=(32+33+…3n+1)+2n=
| 9 |
| 2 |
即数列{kn}的通项公式为:kn=3n+1+2,其前n项的和为
| 9 |
| 2 |
点评:本题给出等差数列的第3项、第5项是等比数列的前2项,求等比数列与等差数列的公共项按原来的顺序构成数列的通项公式.着重着重考查了等差、等比数列的通项公式和等比数列前n项和公式等知识,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
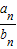 }的前n项和Sn.
}的前n项和Sn.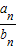 }的前n项和Sn.
}的前n项和Sn.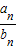 }的前n项和Sn.
}的前n项和Sn.