题目内容
设函数F(x)=(1)求证:0≤![]() <1;
<1;
(2)若函数F(x)的递增区间为[s,t],求|s-t|的取值范围;?
(3)若当x≥k时,(k是与a,b,c无关的常数),恒有F′(x)+a<0,试求k的最小值.
(1)证明:f′(x)=ax2+bx+c,由题意,得f′(1)=a+b+c=0, ①?
f′(M)=aM2+bM+c=-a, ②?
又a<b<c,得3a<a+b+c<
由①得c=-a-b,代入a<b<c,得a<b<-a-b.?
由a<0得-![]() <
<![]() <1. ?
<1. ?
将c=-a-b代入②得,aM2+bM-b=0. ③?
由③有实根,得Δ=b2+4AB≥0,?
即(![]() )2+4
)2+4![]() ≥0.?
≥0.?
解得![]() ≤-4或
≤-4或![]() ≥0. ?
≥0. ?
综上,0≤![]() <1. ?
<1. ?
(2)解:由f′(x)=ax2+bx+c的判别式Δ=b2-4AC>0得f′(x)=ax2+bx+c=0有两个不等实根,?
设为x1,x2,?
又f′(1)=0知x1=1是方程的根,?
∴x2=-![]() -1<0<x1.?
-1<0<x1.?
当x<x2或x>x1时,f′(x)<0;当x2<x<x1时,f′(x)>0. ?
∴函数f(x)的递增区间为[x2,x1].?
∴|s-T|=|x1-x2|=2+![]() ∈[2,3). ?
∈[2,3). ?
(3)解:由f′(x)+a<0,即ax2+bx+c+a<0,即ax2+bx-b<0,?
∵a<0,∴x2+![]() x-
x-![]() >0.?
>0.?
设g(![]() )=(x-1)·
)=(x-1)·![]() +x2对0≤
+x2对0≤![]() <1恒成立. ?
<1恒成立. ?
∴![]() 即
即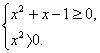
解之,得x≤![]() 或x≥
或x≥![]() . ?
. ?
∴k≥![]() .因此k的最小值为
.因此k的最小值为![]() .
.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案