题目内容
(本小题满分16分)
已知数列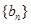 满足
满足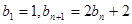 ,
,
(1)求证:数列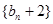 为等比数列 (2)求数列
为等比数列 (2)求数列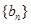 的通项公式
的通项公式
(3)试问:数列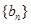 中是否存在不同的三项恰好成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在不同的三项恰好成等差数列?若存在,求出这三项;若不存在,请说明理由.
已知数列
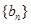 满足
满足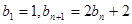 ,
,(1)求证:数列
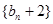 为等比数列 (2)求数列
为等比数列 (2)求数列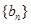 的通项公式
的通项公式(3)试问:数列
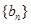 中是否存在不同的三项恰好成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在不同的三项恰好成等差数列?若存在,求出这三项;若不存在,请说明理由.(1) ∵ ,∴
,∴
所以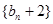 是以
是以 为首项,2为公比的等比数列....5分
为首项,2为公比的等比数列....5分
(2)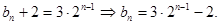 ...........10分
...........10分
(3)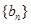 中不存在不同的三项
中不存在不同的三项 恰好成等差数列.
恰好成等差数列.
 ,∴
,∴
所以
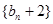 是以
是以 为首项,2为公比的等比数列....5分
为首项,2为公比的等比数列....5分(2)
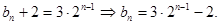 ...........10分
...........10分(3)
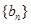 中不存在不同的三项
中不存在不同的三项 恰好成等差数列.
恰好成等差数列. 试题分析:(1)由
 ,得
,得 ,
,根据等比数列的定义可知
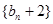 是等比数列.
是等比数列.(2)在(1)的基础上,可求出
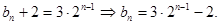
(3)解本小题的关键:假设数列
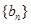 中存在不同的三项
中存在不同的三项 恰好成等差数列,显然
恰好成等差数列,显然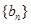 是递增数列,然后可设
是递增数列,然后可设 ,则
,则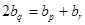 即
即 ,进而得到
,进而得到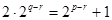 ,
,然后再根据p,q,r取正整数值,并且还要从奇偶性判断是否存在.
(1) ∵
 ,∴
,∴
所以
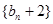 是以
是以 为首项,2为公比的等比数列....5分
为首项,2为公比的等比数列....5分(2)
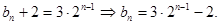 ...........10分
...........10分(3)若数列
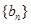 中存在不同的三项
中存在不同的三项 恰好成等差数列,显然
恰好成等差数列,显然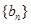 是递增数列,不妨设
是递增数列,不妨设 ,则
,则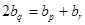
即
 ,化简得:
,化简得: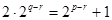 ……(*)................14分
……(*)................14分由于
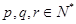 ,且
,且 ,知
,知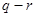 ≥1,
≥1, ≥2,
≥2,所以(*)式左边为偶数,右边为奇数, 故数列
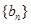 中不存在不同的三项
中不存在不同的三项 恰好成等差数列..16分
恰好成等差数列..16分点评:等比数列的定义是判定一个数列是否是等比数列的依据,勿必理解掌握.对于探索性问题可先假设存在,然后根据条件探索存在应满足的条件,从而最终得出结论.

练习册系列答案
相关题目
 中,
中,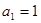 ,
,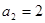 ,数列
,数列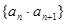 是公比为
是公比为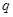 (
(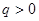 )的等比数列。
)的等比数列。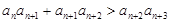 成立的
成立的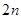 项的和
项的和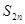 .
.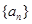 的公比为正数,且
的公比为正数,且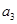
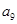 =2
=2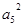 ,
,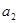 =1,则
=1,则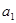 =( )
=( )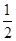
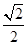
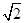
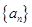 的前
的前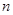 项和为
项和为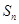 ,
,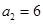 ,
,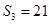 ,求数列
,求数列 中,已知
中,已知 ,且
,且 ________.
________.  中,已知
中,已知 ,则该数列的前12项的和为 .
,则该数列的前12项的和为 . =1,
=1, =3,则
=3,则 的值是 .
的值是 .  中,
中, ,则数列
,则数列