题目内容
已知数列{an}:a1,a2,a3,…,an,…,构造一个新数列:a1,(a2-a1),(a3-a2),…,(an-an-1),…,此数列是首项为1,公比为(1)求数列{an}的通项;
(2)求数列{an}的前n项和Sn.
思路分析:通过观察,不难发现,新数列的前n项和恰为an,这样即可将问题转化为首项为1,公比为![]() 的等比数列的前n项和.数列{an}的通项公式求出后,计算其前n项和Sn就容易多了.
的等比数列的前n项和.数列{an}的通项公式求出后,计算其前n项和Sn就容易多了.
解:(1)an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+![]() +(
+(![]() )2+…+(
)2+…+(![]() )n-1
)n-1
=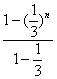 =
=![]() [1-(
[1-(![]() )n].
)n].
(2)Sn=a1+a2+a3+…+an
=![]() (1-
(1-![]() )+
)+![]() [1-(
[1-(![]() )2]+
)2]+![]() [1-(
[1-(![]() )3]+…+
)3]+…+![]() [1-(
[1-(![]() )n]
)n]
=![]() {n-
{n-![]() [1+
[1+![]() +(
+(![]() )2+…+(
)2+…+(![]() )n-1]}
)n-1]}
=![]() n-
n-![]() ·
·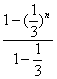
=![]() n-
n-![]() [1-(
[1-(![]() )n]=
)n]=![]() (2n-1)+
(2n-1)+![]() (
(![]() )n-1.
)n-1.

练习册系列答案
相关题目