题目内容
19.已知抛物线y2=2px(p>0)截直线y=2x-4所得弦长$|{AB}|=3\sqrt{5}$,( I)求抛物线的方程;
( II)设F是抛物线的焦点,求△ABF的外接圆上的点到直线AB的最大距离.
分析 (Ⅰ)设A(x1,y1),B(x2,y2),由$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=2x-4}\end{array}\right.$,利用韦达定理以及弦长公式求解p.得到抛物线的方程即可.
(Ⅱ)由(I) 得A(1,-2),B(4,4),F(1,0)求出△ABF的外接圆的方程,然后求解△ABF的外接圆上的点到直线AB的最大距离.
解答 解 (Ⅰ)设A(x1,y1),B(x2,y2),由$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=2x-4}\end{array}\right.$,得4x2-(16+2p)x+16=0,
由根与系数的关系得x1+x2=$\frac{16+2p}{4}$,x1x2=4,
|AB|=$\sqrt{1+{k}^{2}}\sqrt{({{x}_{1}+{x}_{2})}^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{5}$$\sqrt{(\frac{8+P}{2})^{2}-16}$=3$\sqrt{5}$,由p>0,得p=2.
所以抛物线的方程为:y2=4x.
(Ⅱ)由(I) 得A(1,-2),B(4,4),F(1,0)
△ABF的外接圆的方程是$(x-\frac{13}{2})^{2}+(y+1)^{2}=\frac{125}{4}$,
则△ABF的外接圆上的点到直线AB的最大距离为圆心到直线的距离与半径的和,即$\frac{10}{\sqrt{5}}+\frac{5\sqrt{5}}{2}$=$\frac{9\sqrt{5}}{2}$.
点评 本题考查抛物线的简单性质的应用,圆的方程的应用,考查转化思想以及计算能力.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
12.一个几何体的三视图如图所示,则该几何体的体积为( )
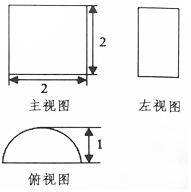

| A. | π | B. | 2π | C. | 2π+4 | D. | 3π+4 |
14.函数$f(x)=\frac{{\sqrt{-lnx}}}{{{x^2}-1}}$的定义域为( )
| A. | (-∞,1) | B. | (0,1) | C. | (0,1] | D. | (-∞,-1)∪(-1,1) |
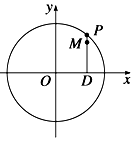 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.