题目内容
已知 ,
, 是非零向量,且满足(
是非零向量,且满足( -2
-2 )⊥
)⊥ ,(
,( -2
-2 )⊥
)⊥ ,则
,则 与
与 的夹角是 °.
的夹角是 °.
【答案】分析:由已知中,( -2
-2 )⊥
)⊥ ,(
,( -2
-2 )⊥
)⊥ ,结合两个向量垂直则数量积为0的原则,我们易得(
,结合两个向量垂直则数量积为0的原则,我们易得( -2
-2 )•
)• =0且(
=0且( -2
-2 )•
)• =0,进而探究出|
=0,进而探究出| |、|
|、| |与
|与 •
• 的关系,然后代入向量夹角公式即可得到答案.
的关系,然后代入向量夹角公式即可得到答案.
解答:解:∵( -2
-2 )⊥
)⊥
∴( -2
-2 )•
)• =0
=0
即 2=2
2=2 •
•
即| |2=2
|2=2 •
• ,|
,| |=
|=
又∵( -2
-2 )⊥
)⊥ ,
,
∴( -2
-2 )•
)• =0
=0
即 2=2
2=2 •
•
即| |2=2
|2=2 •
• ,|
,| |=
|=
∴cosθ= =
=
∴θ=60°
故答案为:60
点评:本题考查的知识点是平面向量数量积的坐标表示、模、夹角,其中cosθ= 是利用向量求角的唯一公式,要求大家熟练掌握.
是利用向量求角的唯一公式,要求大家熟练掌握.
 -2
-2 )⊥
)⊥ ,(
,( -2
-2 )⊥
)⊥ ,结合两个向量垂直则数量积为0的原则,我们易得(
,结合两个向量垂直则数量积为0的原则,我们易得( -2
-2 )•
)• =0且(
=0且( -2
-2 )•
)• =0,进而探究出|
=0,进而探究出| |、|
|、| |与
|与 •
• 的关系,然后代入向量夹角公式即可得到答案.
的关系,然后代入向量夹角公式即可得到答案.解答:解:∵(
 -2
-2 )⊥
)⊥
∴(
 -2
-2 )•
)• =0
=0即
 2=2
2=2 •
•
即|
 |2=2
|2=2 •
• ,|
,| |=
|=
又∵(
 -2
-2 )⊥
)⊥ ,
,∴(
 -2
-2 )•
)• =0
=0即
 2=2
2=2 •
•
即|
 |2=2
|2=2 •
• ,|
,| |=
|=
∴cosθ=
 =
=
∴θ=60°
故答案为:60
点评:本题考查的知识点是平面向量数量积的坐标表示、模、夹角,其中cosθ=
 是利用向量求角的唯一公式,要求大家熟练掌握.
是利用向量求角的唯一公式,要求大家熟练掌握. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 是非零向量,且满足
是非零向量,且满足 ,
, ,则
,则 B.
B. C.
C. D.
D.
 ,
, 是非零向量,且
是非零向量,且 ,则向量
,则向量 与
与 的夹角为 .
的夹角为 . ,
, 是非零向量,且满足(
是非零向量,且满足( -2
-2 )⊥
)⊥ ,(
,( -2
-2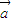 )⊥
)⊥ ,则
,则 与
与 的夹角是 .
的夹角是 . ,
, 是非零向量,且满足(
是非零向量,且满足( -2
-2 )⊥
)⊥ ,(
,( -2
-2 )⊥
)⊥ ,则
,则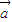 与
与 的夹角是 .
的夹角是 .