题目内容
已知 ,
, 是非零向量,且满足(
是非零向量,且满足( -2
-2 )⊥
)⊥ ,(
,( -2
-2 )⊥
)⊥ ,则
,则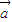 与
与 的夹角是 .
的夹角是 .
【答案】分析:由两个向量垂直的性质可得  ,
, ,从而得到|
,从而得到| |=|
|=| |,故
|,故 即|
即| |•|
|•| |=2|
|=2| |•|
|•| |cosθ,求出 cosθ 的值,从而得到θ的值.
|cosθ,求出 cosθ 的值,从而得到θ的值.
解答:解:设 与
与 的夹角是θ,∵(
的夹角是θ,∵( -2
-2 )⊥
)⊥ ,∴(
,∴( -2
-2 )•
)• =0,∴
=0,∴ .
.
同理,由( -2
-2 )⊥
)⊥ ,可得
,可得 ,∴|
,∴| |=|
|=| |.
|.
故 即|
即| |•|
|•| |=2|
|=2| |•|
|•| |cosθ,∴cosθ=
|cosθ,∴cosθ= ,∴θ=60°.
,∴θ=60°.
故答案为:60°.
点评:本题主要考查两个向量的数量积的定义,两个向量垂直的性质,根据三角函数的值求角,求得| |=|
|=| |是解题的关键,属于中档题.
|是解题的关键,属于中档题.
 ,
, ,从而得到|
,从而得到| |=|
|=| |,故
|,故 即|
即| |•|
|•| |=2|
|=2| |•|
|•| |cosθ,求出 cosθ 的值,从而得到θ的值.
|cosθ,求出 cosθ 的值,从而得到θ的值.解答:解:设
 与
与 的夹角是θ,∵(
的夹角是θ,∵( -2
-2 )⊥
)⊥ ,∴(
,∴( -2
-2 )•
)• =0,∴
=0,∴ .
.同理,由(
 -2
-2 )⊥
)⊥ ,可得
,可得 ,∴|
,∴| |=|
|=| |.
|.故
 即|
即| |•|
|•| |=2|
|=2| |•|
|•| |cosθ,∴cosθ=
|cosθ,∴cosθ= ,∴θ=60°.
,∴θ=60°.故答案为:60°.
点评:本题主要考查两个向量的数量积的定义,两个向量垂直的性质,根据三角函数的值求角,求得|
 |=|
|=| |是解题的关键,属于中档题.
|是解题的关键,属于中档题. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, 是非零向量,且满足
是非零向量,且满足 ,
, ,则
,则 B.
B. C.
C. D.
D.
 ,
, 是非零向量,且
是非零向量,且 ,则向量
,则向量 与
与 的夹角为 .
的夹角为 . ,
, 是非零向量,且满足(
是非零向量,且满足( -2
-2 )⊥
)⊥ ,(
,( -2
-2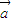 )⊥
)⊥ ,则
,则 与
与 的夹角是 .
的夹角是 . ,
, 是非零向量,且满足(
是非零向量,且满足( -2
-2 )⊥
)⊥ ,(
,( -2
-2 )⊥
)⊥ ,则
,则 与
与 的夹角是 °.
的夹角是 °.