题目内容
顶点在原点,焦点在x轴上,且截直线2x-y+1=0所得弦长为![]() ,求抛物线方程.
,求抛物线方程.
y2=12x或y2=-4x.
解析:
设所求抛物线方程为y2=ax(a≠0), ①
直线方程变形为y=2x+1. ②
设抛物线截直线所得弦长为|AB|,且A(x1,y1),B(x2,y2).
②代入①并整理得4x2+(4-a)x+1=0.
由韦达定理得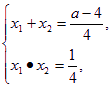
∴|AB|=![]() .
.
解得a=12或a=-4.∴所求抛物线方程为y2=12x或y2=-4x.

练习册系列答案
相关题目
顶点在原点、焦点在x轴上的抛物线被直线y=x+1截得的弦长是
,则抛物线的方程是( )
| 10 |
| A、y2=-x或y2=5x |
| B、y2=-x |
| C、y2=x或y2=-5x |
| D、y2=5x |
 已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.
已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.