题目内容
已知圆C:![]() ,是否存在斜率为1的直线L,使L被圆C截得的弦AB为直径的圆过原点,若存在求出直线L的方程,若不存在说明理由.
,是否存在斜率为1的直线L,使L被圆C截得的弦AB为直径的圆过原点,若存在求出直线L的方程,若不存在说明理由.
圆C化成标准方程为:![]()
假设存在以AB为直径的圆M,圆心M的坐标为(a,b)
由于CM⊥L,∴kCM×kL=-1 ∴kCM=![]() ,
,
即a+b+1=0,得b= -a-1 ①
直线L的方程为y-b=x--,即x-y+b-a=0 ∴ CM=![]()
∵以AB为直径的圆M过原点,∴![]()
![]() ,
,![]()
∴![]() ②
②
把①代入②得 ![]() ,∴
,∴![]()
当![]() 此时直线L的方程为:x-y-4=0;当
此时直线L的方程为:x-y-4=0;当![]() 此时直线L的方程为:x-y+1=0
此时直线L的方程为:x-y+1=0
故这样的直线L是存在的,方程为x-y-4=0 或x-y+1=0.
解析:
同答案

练习册系列答案
相关题目
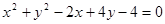 ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。 ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。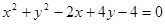 ,是否存在斜率为1的直线
,是否存在斜率为1的直线 ,使以
,使以