题目内容
(本小题满分13分)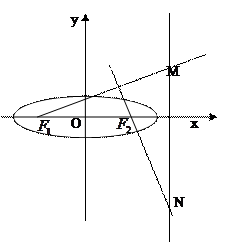 设椭圆
设椭圆 的左右焦点分别为
的左右焦点分别为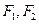 ,离心率
,离心率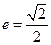 ,过
,过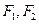 分别作直线
分别作直线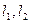 ,且
,且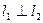 ,
,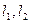 分别交直线
分别交直线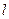 :
: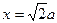 于
于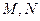 两点。
两点。
(Ⅰ)若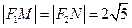 ,求 椭圆的方程;
,求 椭圆的方程;
(Ⅱ)当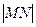 取最小值时,试探究
取最小值时,试探究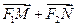 与
与
的关系,并证明之.
 设椭圆
设椭圆 的左右焦点分别为
的左右焦点分别为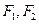 ,离心率
,离心率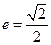 ,过
,过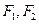 分别作直线
分别作直线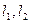 ,且
,且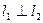 ,
,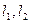 分别交直线
分别交直线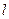 :
: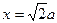 于
于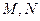 两点。
两点。 (Ⅰ)若
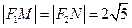 ,求 椭圆的方程;
,求 椭圆的方程;(Ⅱ)当
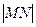 取最小值时,试探究
取最小值时,试探究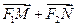 与
与
的关系,并证明之.
(Ⅰ) (Ⅱ) 共线
(Ⅱ) 共线
 (Ⅱ) 共线
(Ⅱ) 共线由 与
与 ,得
,得
 ,
,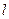 的方程为
的方程为 设
设
则 由
由 得
得  ①
①
(Ⅰ)由 ,得
,得 ②
②
 ③由①、②、③三式,消去
③由①、②、③三式,消去 ,并求得
,并求得
故 所以所求的椭圆方程为
所以所求的椭圆方程为 ……7分
……7分
(Ⅱ)
当且仅当 或
或 时,
时,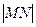 取最小值
取最小值
此时,
故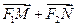 与
与 共线。 ……13分
共线。 ……13分
 与
与 ,得
,得
 ,
,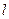 的方程为
的方程为 设
设
则
 由
由 得
得  ①
①(Ⅰ)由
 ,得
,得 ②
② ③由①、②、③三式,消去
③由①、②、③三式,消去 ,并求得
,并求得
故
 所以所求的椭圆方程为
所以所求的椭圆方程为 ……7分
……7分(Ⅱ)

当且仅当
 或
或 时,
时,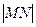 取最小值
取最小值
此时,

故
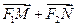 与
与 共线。 ……13分
共线。 ……13分
练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
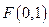 ,直线
,直线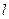 :
: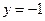 ,
,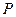 为平面上的动点,过点
为平面上的动点,过点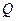 ,且
,且 .
.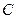 的方程;
的方程;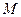 过定点
过定点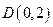 ,圆心
,圆心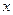 轴交于
轴交于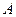 、
、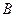 两点,设
两点,设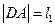 ,
, ,求
,求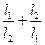 的最大值.
的最大值.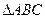 的两个顶点分别
的两个顶点分别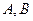 的坐标为
的坐标为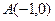 ,
,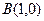 ,平面内两点
,平面内两点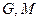 同时满足下列条件:
同时满足下列条件: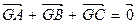 ;②
;②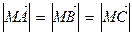 ;③
;③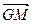 ∥
∥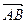
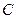 的轨迹方程;
的轨迹方程;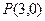 的直线
的直线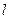 与(1)中轨迹交于
与(1)中轨迹交于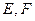 两点,求
两点,求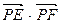 的取值范围
的取值范围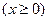 上
上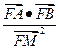 的值
的值 平面上,
平面上,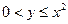 ,
,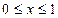 所围成图形的面积为
所围成图形的面积为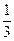 ,则集合
,则集合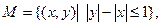
 的交集
的交集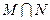 所表示的图形面积为
所表示的图形面积为  (C)
(C)  (B)
(B) 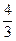 . ( )
. ( )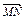 ||
||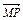 |+
|+ 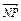 =0,求动点P(x,y)的轨迹方程.
=0,求动点P(x,y)的轨迹方程.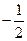 ,则M等于( )
,则M等于( )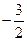
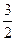
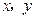 满足
满足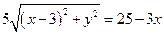 ,求
,求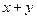 的最大值与最小值.
的最大值与最小值.