题目内容
【题目】如图甲所示,![]() 是梯形
是梯形![]() 的高,
的高,![]() ,
,![]() ,
,![]() ,先将梯形
,先将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() .
.
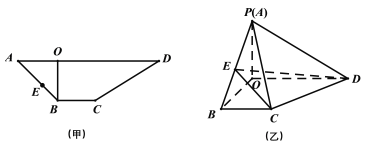
(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)点![]() 是线段
是线段![]() 上一动点,当直线
上一动点,当直线![]() 与
与![]() 所成的角最小时,求二面角
所成的角最小时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() ,详见解析(2)
,详见解析(2)![]()
【解析】
(1)过![]() 作
作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,易得
,易得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ,所以得到
,所以得到![]() 平面
平面![]() ,而此时根据几何关系可以得到
,而此时根据几何关系可以得到![]() ;(2)以
;(2)以![]() 为坐标原点建立空间直角坐标系,
为坐标原点建立空间直角坐标系,![]() ,表示出
,表示出![]() 与
与![]() 所成角为
所成角为![]() 的余弦值,并求出
的余弦值,并求出![]() 最小时
最小时![]() 的值,从而得到各点坐标,再求出平面
的值,从而得到各点坐标,再求出平面![]() 和平面
和平面![]() 的法向量,根据两个法向量之间的夹角公式,求得答案.
的法向量,根据两个法向量之间的夹角公式,求得答案.
解:(1)存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() ,理由如下:
,理由如下:
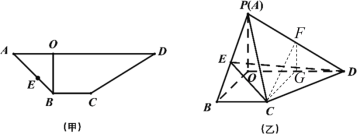
依题,![]() ,
,![]() ,
,![]() ,
,
即![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
所以![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
因为![]() ,
,![]() ,
,![]()
所以![]() ,
,
所以![]() ,
,
而![]() ,所以有
,所以有![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
而![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
故存在点![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]()
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
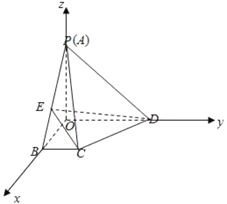
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]()
即![]() ,所以
,所以![]() ,
,
![]() ,
,![]()
设直线![]() 与
与![]() 所成角为
所成角为![]()
则![]()
令![]() ,则
,则![]() ,
,
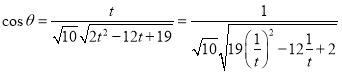
令![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() 取最大值,
取最大值,
此时直线![]() 与
与![]() 所成的角最小.此时
所成的角最小.此时![]() .
.
所以![]() ,又因为
,又因为![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 法向量分别为
法向量分别为![]()
则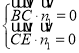 ,即
,即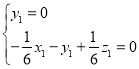
取![]() 得平面
得平面![]() 的法向量为
的法向量为![]() ,
,
设平面![]() 法向量为
法向量为![]()
则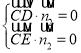 ,即
,即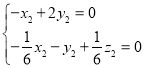
取![]() 得平面
得平面![]() 法向量为
法向量为![]()
所以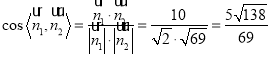 ,
,
由图可知,二面角![]() 为钝二面角,则其余弦值为
为钝二面角,则其余弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

