题目内容
8.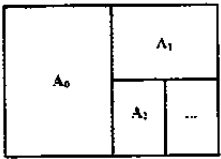 An(n∈N)系列的纸张规格如图,其特色在于:
An(n∈N)系列的纸张规格如图,其特色在于:①A0,A1,A2,…,An所有规格的纸张的长宽比都相同;
②A0对裁后可以得到两张A1,A1对裁后可以得到两张A2,…,An-1对裁后可以得到两张An.
现有每平方厘米重量为b克的A0,A1,A2,…,An纸各一张,若A4纸的宽度为a厘米,则这(n+1)张纸的重量之和Sn+1等于$32\sqrt{2}{a^2}b[{1-{{(\frac{1}{2})}^{n+1}}}]$.(单位:克)
分析 由题意可得面积是逐渐变为上一个的一半,由相似可得x:y=$\sqrt{2}$:1,由此能求出这(n+1)张纸的重量之和Sn+1.
解答 解:由题意可得面积是逐渐变为上一个的一半,设An的长、宽分别为x,y,则An+1的长、宽分别为y,$\frac{1}{2}$x,
由相似可得x:y=$\sqrt{2}$:1,
故A4的面积为$\sqrt{2}$a2,A1的面积为8$\sqrt{2}$a2,A0的面积为16$\sqrt{2}{a}^{2}$,
所以Sn+1=$\frac{8\sqrt{2}{a}^{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}•b$+16$\sqrt{2}{a}^{2}b$
=16$\sqrt{2}$a2b(2-$\frac{1}{{2}^{n}}$)
=$32\sqrt{2}{a^2}b[{1-{{(\frac{1}{2})}^{n+1}}}]$.
故答案为:$32\sqrt{2}{a^2}b[{1-{{(\frac{1}{2})}^{n+1}}}]$.
点评 本题考查等比数列的求和,归纳推理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
19.已知函数f(x+1)为定义在R上的偶函数,且当f(x)在[1,+∞)上为增函数,若a=20.1-1,b=1-2-0.1,则f(a)与f(b)的大小关系为( )
| A. | f(a)>f(b) | B. | f(a)<f(b) | ||
| C. | f(a)=f(b) | D. | f(a)与f(b)的大小不确定 |
16.高三一班共选出共有5个节目参加学校的文艺汇演,其中3个舞蹈节目,2个小品节目;如果2个小品节目不能连续出场,且舞蹈节目甲不能在第一个出场,那么出场顺序的排法种数为( )
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
17.已知等比数列{an}中,a1=3,8an2=an+1•an+2,则a3=( )
| A. | 2 | B. | 6 | C. | 12 | D. | 48 |
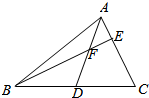 △ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求:
△ABC中,D为BC的中点,E为AC边上靠近点A的一个三等分点,AD与BE交于点F,求: