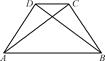
题目内容
已知圆O的内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一
点,AE为圆O的切线,求证:CD2=BD·EC.
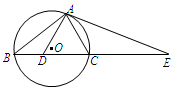
点,AE为圆O的切线,求证:CD2=BD·EC.

详见解析
试题分析:根据圆的几何性质有:
 为圆
为圆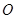 的切线,所以
的切线,所以 ,又由
,又由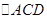 为等边三角形,所以
为等边三角形,所以 ,由相似三角形的条件可得
,由相似三角形的条件可得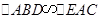 ,可得:
,可得: ,即
,即 ,再由
,再由 ,即可得
,即可得 .
. 试题解析:因为
 为圆
为圆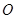 的切线,所以
的切线,所以 . 2分
. 2分因为
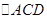 为等边三角形,所以
为等边三角形,所以 ,
,所以
 所以
所以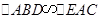 . 6分
. 6分所以
 ,即
,即 . 8分
. 8分因为
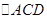 为等边三角形,所以
为等边三角形,所以 ,
, 所以
 . 10分
. 10分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 B.
B. C.
C. D.
D. 或
或
 ,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
,C是圆O外一点,AC交圆O于点E,BC交圆O于点D,已知AC=AB,BC=4,求△ADE的周长.
