题目内容
如图，在四边形ABCD中，△ABC≌△BAD.求证：AB∥CD.
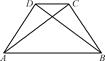
见解析
证明：由△ABC≌△BAD得∠ACB＝∠BDA，
故A、B、C、D四点共圆，
从而∠CAB＝∠CDB.
再由△ABC≌△BAD得∠CAB＝∠DBA.
因此∠DBA＝∠CDB，所以AB∥CD.
故A、B、C、D四点共圆，
从而∠CAB＝∠CDB.
再由△ABC≌△BAD得∠CAB＝∠DBA.
因此∠DBA＝∠CDB，所以AB∥CD.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
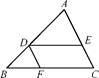
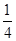AD，N是AB的中点，NF⊥CE于F，求证：FN2＝EF·FC.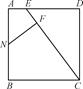
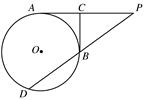
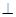PD.若PC=4， PB=2，则CD=____________.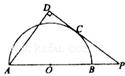
在
上，
，则
________．
