题目内容
13.过点M(1,3)引圆x2+y2=2的切线,切点分别为A,B,则sin∠AMB=( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
分析 作出图象易得sin∠OMB,cos∠OMB的值,再利用二倍角计算sin∠AMB的值.
解答 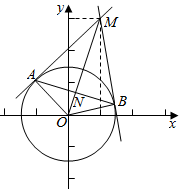 解:如图所示,由题意可得|OM|=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,
解:如图所示,由题意可得|OM|=$\sqrt{{1}^{2}{+3}^{2}}$=$\sqrt{10}$,
|OB|=r=$\sqrt{2}$;
由勾股定理可得|MA|=|MB|=$\sqrt{10-2}$=2$\sqrt{2}$,
∴sin∠OMB=$\frac{OB}{OM}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$,
∴cos∠OMB=$\frac{BM}{OM}$=$\frac{2\sqrt{2}}{\sqrt{10}}$=$\frac{2\sqrt{5}}{5}$,
∴sin∠AMB=sin2∠OMB
=2sin∠OMBcos∠OMB
=2×$\frac{\sqrt{5}}{5}$×$\frac{2\sqrt{5}}{5}$
=$\frac{4}{5}$.
故选:C.
点评 本题考查了圆的切线问题,涉及勾股定理和二倍角公式的应用问题,是基础题.

练习册系列答案
相关题目
4.某大学中文系有学生5200人,其中一年级学生2000人、二年级学生1600人、三年级学生1200人、四年级学生400人,要用分层抽样的方法从该系中抽取一个容量为260的样本,则应抽三年级的学生( )
| A. | 100人 | B. | 60人 | C. | 80人 | D. | 20人 |
8.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
若由资料知,y与x呈线性相关关系,
(1)试求线性回归方程$\left.\begin{array}{l}{∧}\\{y}\end{array}\right.$=$\left.\begin{array}{l}{∧}\\{b}\end{array}\right.$x+$\left.\begin{array}{l}{∧}\\{a}\end{array}\right.$.( 提示:$\left.\begin{array}{l}{∧}\\{b}\end{array}\right.$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i-1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$; $\left.\begin{array}{l}{∧}\\{a}\end{array}\right.$=$\overline{y}$-$\left.\begin{array}{l}{∧}\\{b}\end{array}\right.$$\overline{x}$)
(2)估计使用年限为10年时,维修费用是多少?
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)试求线性回归方程$\left.\begin{array}{l}{∧}\\{y}\end{array}\right.$=$\left.\begin{array}{l}{∧}\\{b}\end{array}\right.$x+$\left.\begin{array}{l}{∧}\\{a}\end{array}\right.$.( 提示:$\left.\begin{array}{l}{∧}\\{b}\end{array}\right.$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i-1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$; $\left.\begin{array}{l}{∧}\\{a}\end{array}\right.$=$\overline{y}$-$\left.\begin{array}{l}{∧}\\{b}\end{array}\right.$$\overline{x}$)
(2)估计使用年限为10年时,维修费用是多少?
2.从甲、乙、丙三名学生中任选两名学生参加某项活动,甲被选中的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |