题目内容
18.设{an}的公比不为1的等比数列,且a5,a3,a4成等差数列.(1)求数列{an}的公比;
(2)若a1=-2,求数列$\left\{{\frac{1}{a_n}}\right\}$的前n项和Sn.
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)利用等比数列的前n项和公式即可得出.
解答 解:(1)设数列{an}的公比为q(q≠0,q≠1),
由a5,a3,a4成等差数列,得到2a3=a5+a4,即$2{a_3}={a_3}{q^2}+{a_3}q$,
由a3≠0,q≠0得q2+q-2=0,
解得q=-2或q=1(舍去),
∴q=-2.
(2)依题意易得$\left\{{\frac{1}{a_n}}\right\}$是以$\frac{1}{a_1}=-\frac{1}{2}$为首项,$-\frac{1}{2}$为公比的等比数列,
∴${S_n}=\frac{{-\frac{1}{2}[{1-{{({-\frac{1}{2}})}^n}}]}}{{1-({-\frac{1}{2}})}}=-\frac{{1-{{({-\frac{1}{2}})}^n}}}{3}$=$\frac{{{{({-\frac{1}{2}})}^n}-1}}{3}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.某班主任对全班50名学生进行了作业量多少的调查,数据如下:
则认为喜欢玩手机与认为作业多少有关系的把握大约为95%.
附:x2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当x2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当x2>2.706时,有90%的把握判定变量A,B有关联;
当x2>3.841时,有95%的把握判定变量A,B有关联;
当x2>6.635时,有99%的把握判定变量A,B有关联.
| 认为作业多 | 认为作业不多 | |
| 喜欢玩手机 | 18 | 9 |
| 不喜欢玩手机 | 7 | 16 |
附:x2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当x2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当x2>2.706时,有90%的把握判定变量A,B有关联;
当x2>3.841时,有95%的把握判定变量A,B有关联;
当x2>6.635时,有99%的把握判定变量A,B有关联.
6.已知数列{an}满足a1=0,an+1=$\frac{{{a_n}-2}}{{\frac{5}{4}{a_n}-2}}$,则a2015=( )
| A. | 0 | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
9.下列四个函数中,在区间(0,$\frac{1}{4}$)上为减函数的是( )
| A. | y=x($\frac{1}{2}$)x | B. | y=-($\frac{1}{2}$)x | C. | y=xlog2x | D. | y=x${\;}^{\frac{1}{3}}$ |
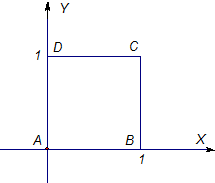 如图,在直角坐标系中,正方形ABCD的四个顶点分别为A(0,0),B(1,0),C(1,1),D(0,1).
如图,在直角坐标系中,正方形ABCD的四个顶点分别为A(0,0),B(1,0),C(1,1),D(0,1). 是定义在实数集
是定义在实数集 上的奇函数,且当
上的奇函数,且当 时,
时, 成立,若
成立,若 ,则
,则 大小关系( )
大小关系( ) B.
B.
 D.
D.
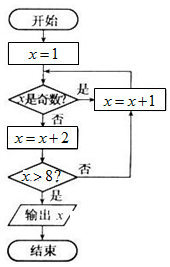
 的零点所在区间是( )
的零点所在区间是( ) B.
B. C.
C. D.
D.