题目内容
（本题满分14分）在边长为3的正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足
，将
沿EF折起到
的位置，使二面角
成直二面角，连结
，
（如图）（I）求证：
(Ⅱ)求点B到面
的距离(Ⅲ)求异面直线BP与
所成角的余弦
(Ⅰ) 见解析 (Ⅱ) 
（Ⅲ）
解析:
（I）在图1中，取BE的中点D，连DF
∵
，∵
∴
为正三角形
又∵AE=ED=1 ∴
∴在图2中有
，
∴
为二面角
的平面角
∵二面角为直二面角 ∴
又∵
∴
即
…………5分
(Ⅱ)∵BE//PF ∴BE//面
∵B到面的距离即为E到面的距离，
∵
，又BE//PF， ∴
∴
∵E到面
的距离即为
中E到
的距离
d=A1E×
∴点B到面的距离为………………10分
(Ⅲ)∵DF//BP ∴
即为所求角
中
,
∴异面直线BP与所成角的余弦值为 ………………14分
法二:(建立空间直角坐标系,略解)
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（
），
，动点
的轨迹为T．
时，已知
、
，试探究是否存在这样的点
： 
？若存在，求出点Q的坐标，若不存在，说明理由．
中，已知圆
，
．
的直线
被圆
截得的弦长为
，求直线
是以1为半径，圆心在圆
：
上移动的动圆 ，若圆
分别作圆
的两条切线
，切点为
，求
的取值范围 ；
同时平分圆
的周长、圆
中，角
、
、
所对应的边分别为
、
、
，且满足
，求实数
的值。
，求
的值.
的正方体
中,
是线段
的中点,底面ABCD的中心是F.
^
； 
；
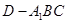的体积。
的左、右焦点分别为F1、F2．F2也是抛物线C2：
的焦点，点M为C1与C2在第一象限的交点，且
．
，直线l∥MN，且与C1交于A、B两点，若
·
=0，求直线l的方程．