题目内容
已知P是抛物线C:x2=2y上异于原点的一点.(1) 过P点的切线l1与x轴、y轴分别交于点M、N,求
 的值;
的值;(2)过P点与切线l1垂直的直线l2与抛物线C交于另一点Q,且与x轴、y轴分别交于点S、T,求
 的取值范围.
的取值范围.
【答案】分析:(1)由P是抛物线C:x2=2y上异于原点的一点,设出点P的坐标,求出抛物线解析式的导函数,把P的横坐标代入导函数求出的导函数值即为切线方程的斜率,由P的坐标和表示出的斜率写出切线的方程,令y=0求出点M的横坐标,又点N的横坐标为0,根据中点坐标公式,得到M为PN的中点,即PM=MN,即可求出 的值;
的值;
(2)设出直线l的方程为y=kx+b,分别过P,Q作PP'⊥x轴,QQ'⊥x轴,垂足分别为P',Q',根据三角形的相似得到所求式子与点P和点Q的纵坐标有关的式子,与抛物线方程联立消去x得到关于y的一元二次方程,利用韦达定理表示出两根之和与两根之积,根据基本不等式把所求式子利用基本不等式化简后,将两根之积代入即可求出所求式子的最小值,进而得到所求式子的取值范围.
解答:解:(1)设点 ,
,
∵y'=x,故过点P的切线方程为 ,
,
令y=0得 ,
,
又N点的横坐标为0,故M为PN的中点,
∴ ;(4分)
;(4分)
(2)设直线l:y=kx+b,由题意k≠0,b≠0则T(0,b)
分别过P,Q作PP'⊥x轴,QQ'⊥x轴,垂足分别为P',Q',
则 ,
,
由 消去x得y2-2(k2+b)y+b2=0
消去x得y2-2(k2+b)y+b2=0
则 (7分)
(7分)
∴ ,(9分)
,(9分)
又y1≠y2,
∴ 的取值范围是(2,+∞).
的取值范围是(2,+∞).
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,灵活运用韦达定理及基本不等式化简求值,灵活运用三角形相似得对应边成比例解决实际问题,是一道中档题.
 的值;
的值;(2)设出直线l的方程为y=kx+b,分别过P,Q作PP'⊥x轴,QQ'⊥x轴,垂足分别为P',Q',根据三角形的相似得到所求式子与点P和点Q的纵坐标有关的式子,与抛物线方程联立消去x得到关于y的一元二次方程,利用韦达定理表示出两根之和与两根之积,根据基本不等式把所求式子利用基本不等式化简后,将两根之积代入即可求出所求式子的最小值,进而得到所求式子的取值范围.
解答:解:(1)设点
 ,
,∵y'=x,故过点P的切线方程为
 ,
,令y=0得
 ,
,又N点的横坐标为0,故M为PN的中点,
∴
 ;(4分)
;(4分)(2)设直线l:y=kx+b,由题意k≠0,b≠0则T(0,b)
分别过P,Q作PP'⊥x轴,QQ'⊥x轴,垂足分别为P',Q',
则
 ,
,由
 消去x得y2-2(k2+b)y+b2=0
消去x得y2-2(k2+b)y+b2=0则
 (7分)
(7分)∴
 ,(9分)
,(9分)又y1≠y2,
∴
 的取值范围是(2,+∞).
的取值范围是(2,+∞).点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,灵活运用韦达定理及基本不等式化简求值,灵活运用三角形相似得对应边成比例解决实际问题,是一道中档题.

练习册系列答案
相关题目
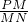 的值;
的值; 的取值范围.
的取值范围.