题目内容
已知P是抛物线C:x2=2y上异于原点的一点.
(1) 过P点的切线l1与x轴、y轴分别交于点M、N,求
的值;
(2)过P点与切线l1垂直的直线l2与抛物线C交于另一点Q,且与x轴、y轴分别交于点S、T,求
+
的取值范围.
(1) 过P点的切线l1与x轴、y轴分别交于点M、N,求
| PM |
| MN |
(2)过P点与切线l1垂直的直线l2与抛物线C交于另一点Q,且与x轴、y轴分别交于点S、T,求
| ST |
| SP |
| ST |
| SQ |
(1)设点P(x0,
) (x0≠0),
∵y'=x,故过点P的切线方程为y-
=x0(x-x0),
令y=0得x=
,
又N点的横坐标为0,故M为PN的中点,
∴
=1;(4分)
(2)设直线l:y=kx+b,由题意k≠0,b≠0则T(0,b)
分别过P,Q作PP'⊥x轴,QQ'⊥x轴,垂足分别为P',Q',
则
+
=
+
=
+
,
由
消去x得y2-2(k2+b)y+b2=0
则
(7分)
∴
+
=
+
≥2b
=2b•
=2,(9分)
又y1≠y2,
∴
+
的取值范围是(2,+∞).
| 1 |
| 2 |
| x | 20 |
∵y'=x,故过点P的切线方程为y-
| 1 |
| 2 |
| x | 20 |
令y=0得x=
| x0 |
| 2 |
又N点的横坐标为0,故M为PN的中点,
∴
| PM |
| MN |
(2)设直线l:y=kx+b,由题意k≠0,b≠0则T(0,b)
分别过P,Q作PP'⊥x轴,QQ'⊥x轴,垂足分别为P',Q',
则
| ST |
| SP |
| ST |
| SQ |
| OT |
| P′P |
| OT |
| Q′Q |
| b |
| y1 |
| b |
| y2 |
由
|
则
|
∴
| ST |
| SP |
| ST |
| SQ |
| b |
| y1 |
| b |
| y2 |
|
| 1 |
| b |
又y1≠y2,
∴
| ST |
| SP |
| ST |
| SQ |

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
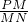 的值;
的值; 的取值范围.
的取值范围. 的值;
的值; 的取值范围.
的取值范围.