Question

已知F₁，F₂分别是椭圆C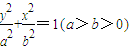：的上、下焦点，其中F₁也是抛物线C₁：x²=4y的焦点，点M是C₁与C₂在第二象限的交点，且．
（1）求椭圆C₁的方程；
（2）已知A（b，0），B（0，a），直线y=kx（k＞0）与AB相交于点D，与椭圆C₁相交于点E，F两点，求四边形AEBF面积的最大值．

Answer 1

【答案】分析：（1）利用抛物线的标准方程即可得出焦点坐标，再利用抛物线的定义和点M在抛物线上即可得到点M的坐标；利用点M在椭圆C₁上满足椭圆的方程和c²=a²-b²即可得到椭圆的方程；
（2）设E（x₁，y₁），F（x₂，y₂），其中x₁＜x₂，由点F满足，及，，故四边形AEBF的面积S=S_△BEF
+S_△AEF==，再利用基本不等式的性质即可得出．
解答：解：（1）由抛物线C₁：x²=4y的焦点，得焦点F₁（1，0）．
设M（x，y）（x＜0），由点M在抛物线上，
∴，，解得，．
而点M在椭圆C₁上，∴，化为，
联立，解得，
故椭圆的方程为．
（2）由（1）可知：|AO|=，|BO|=2．设E（x₁，y₁），F（x₂，y₂），其中x₁＜x₂，
把y=kx代人，可得，x₂＞0，y₂=-y₁＞0，且．
，，
故四边形AEBF的面积S=S_△BEF+S_△AEF==
=≤=．
当且仅当时上式取等号．
∴四边形AEBF面积的最大值为．
点评：本题综合考查了椭圆抛物线的标准方程及其性质、直线与椭圆相交问题、四边形的面积转化为三角形的面积计算、基本不等式的性质等基础知识与方法，需要较强的推理能力和计算能力．