题目内容
三次函数
 在区间
在区间 上是减函数,那么
上是减函数,那么 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
D
解析试题分析:对三次函数 求导,得
求导,得 ,因为函数在区间
,因为函数在区间 上是减函数,所以
上是减函数,所以 ,画出可行域知,
,画出可行域知, 的最大值为
的最大值为 .
.
考点:1.导数;2.线性规划.

练习册系列答案
相关题目
设 的两个极值点分别是
的两个极值点分别是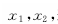 若
若
 (-1,0),则2a+b的取值范围是( )
(-1,0),则2a+b的取值范围是( )
| A.(1,7) | B.(2,7) | C.(1,5) | D.(2,5) |
已知x,y满足约束条件 则
则 的最小值是( )
的最小值是( )
| A.-20 | B.-10 | C.-15 | D.0 |
已知点 在不等式组
在不等式组 表示的平面区域上运动,则
表示的平面区域上运动,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知实数 满足
满足 ,且目标函数
,且目标函数 的最大值为
的最大值为 ,最小值为
,最小值为 , 其中
, 其中 的值为( )
的值为( )
| A.4 | B.3 | C.2 | D.1 |
当实数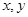 满足不等式
满足不等式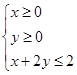 时,恒有
时,恒有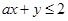 成立,则实数
成立,则实数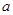 的取值集合是( )
的取值集合是( )
A. | B. | C.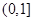 | D.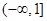 |
已知变量 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 仅在点
仅在点 处取到最大值,则实数
处取到最大值,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
直线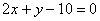 与不等式组
与不等式组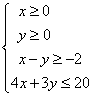 表示的平面区域的公共点有
表示的平面区域的公共点有
A.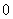 个 个 | B.1个 | C.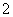 个 个 | D.无数个 |
 ,过点P的直线l与圆
,过点P的直线l与圆 相交于A、B两点,则
相交于A、B两点,则 的最小值为( )
的最小值为( )  D.
D.