题目内容
设 的两个极值点分别是
的两个极值点分别是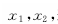 若
若
 (-1,0),则2a+b的取值范围是( )
(-1,0),则2a+b的取值范围是( )
| A.(1,7) | B.(2,7) | C.(1,5) | D.(2,5) |
B.
解析试题分析:
 由可行域知
由可行域知 故选B.
故选B.
考点:1.函数极值与导数;2.一元二次方程根的分布问题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
设变量x,y满足约束条件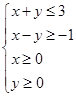 且目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,则a+b=( )
且目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,则a+b=( )
| A.10 | B.-2 | C.8 | D.6 |
已知变量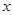 ,
,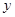 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( )
| A.3 | B.1 | C.-5 | D.-6 |
已知 满足约束条件
满足约束条件 则
则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
若 、
、 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( )
| A.20 | B.22 | C.24 | D.28 |
已知点 的坐标满足条件
的坐标满足条件 ,那么
,那么 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
三次函数
 在区间
在区间 上是减函数,那么
上是减函数,那么 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
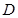 由以
由以 、
、 、
、 为顶点的三角形内部和边界组成.若在区域
为顶点的三角形内部和边界组成.若在区域 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则 ( )
( )


 上的函数
上的函数 满足
满足 ,
, 为
为 的图像如图所示,若两个正数
的图像如图所示,若两个正数 、
、 满足
满足 ,则
,则 的取值范围是 ( )
的取值范围是 ( )



