题目内容
2.已知a>b>0,a+b=1,则$\frac{4}{a-b}+\frac{1}{2b}$的最小值等于9.分析 化简$\frac{4}{a-b}+\frac{1}{2b}$=$\frac{4(a-b+2b)}{a-b}$+$\frac{a-b+2b}{2b}$=4+4•$\frac{2b}{a-b}$+$\frac{a-b}{2b}$+1,从而利用基本不等式求最值.
解答 解:∵a>b>0,a+b=1,
∴a-b>0,a-b+2b=1,
∴$\frac{4}{a-b}+\frac{1}{2b}$
=$\frac{4(a-b+2b)}{a-b}$+$\frac{a-b+2b}{2b}$
=4+4•$\frac{2b}{a-b}$+$\frac{a-b}{2b}$+1
=4•$\frac{2b}{a-b}$+$\frac{a-b}{2b}$+5≥9,
(当且仅当4•$\frac{2b}{a-b}$=$\frac{a-b}{2b}$,即a=$\frac{5}{6}$,b=$\frac{1}{6}$时,等号成立),
故答案为:9.
点评 本题考查了不等式的性质及应用,同时考查了整体思想与转化思想的应用,属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
10.分别从A网和B网上对某一型号家用电器的日销售量(单位:台)进行统计,最近50天的统计结果知下:
(A网)
(B网)
若以上表中频率作为概率,且每天的销售量相互独立.
(1)这两个平台,哪一个平台该产品的销售量更稳定些;
(2)以A网为研究对象,已知每台该电器的销售利润为0.2(千元),用ξ表示该种电器2天销售利润的和(单位:千元),求ξ的分布列和数学期望.
| 日销售量(台) | 100 | 150 | 200 |
| 频数 | 10 | 25 | 15 |
| 频率 | 0.2 | 0.5 | 0.3 |
| 日销售量(台) | 100 | 150 | 200 |
| 频数 | 15 | 15 | 20 |
| 频率 | 0.3 | 0.3 | 0.4 |
若以上表中频率作为概率,且每天的销售量相互独立.
(1)这两个平台,哪一个平台该产品的销售量更稳定些;
(2)以A网为研究对象,已知每台该电器的销售利润为0.2(千元),用ξ表示该种电器2天销售利润的和(单位:千元),求ξ的分布列和数学期望.
14.若圆C1:x2+y2+ax=0与圆C2:x2+y2+2ax+ytanθ=0都关于直线2x-y-1=0对称,则sinθcosθ=( )
| A. | $\frac{2}{5}$ | B. | -$\frac{6}{37}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{2}{3}$ |
11.已知两点A(-3,$\sqrt{3}$),B($\sqrt{3}$,-1),则直线AB的倾斜角θ等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5}{6}π$ |
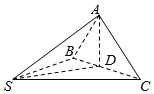 如图所示,在四面体S-ABC中,SA=SB=SC=1,∠ASB=∠ASC=60°,∠BSC=90°,D是BC的中点.求证:
如图所示,在四面体S-ABC中,SA=SB=SC=1,∠ASB=∠ASC=60°,∠BSC=90°,D是BC的中点.求证: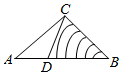 如图,B、C两点之间不能直接到达,为测量B、C两点间的距离(单位:千米),先确定一条直线AD,使得A、D、B三点共线,且∠ADC为钝角,现测得∠BCD=60°,∠A=45°,CD=$\sqrt{6}$-$\sqrt{2}$,AC=$\sqrt{2}$,∠CDB=θ.
如图,B、C两点之间不能直接到达,为测量B、C两点间的距离(单位:千米),先确定一条直线AD,使得A、D、B三点共线,且∠ADC为钝角,现测得∠BCD=60°,∠A=45°,CD=$\sqrt{6}$-$\sqrt{2}$,AC=$\sqrt{2}$,∠CDB=θ.