题目内容
已知双曲线的虚轴长为6,焦点F到实轴的一个端点的距离等于9,则双曲线的离心率等于( )
分析:根据双曲线的虚轴长为6,得到b=3,从而c2-a2=9,再根据焦点F到实轴的一个端点的距离等于9,得到c±a=9.然后分两种情况讨论,解方程组得a=4,c=5,最后可得双曲线的离心率.
解答:解:∵双曲线的虚轴长为6,
∴2b=6⇒b=3⇒c2-a2=32=9…①
又∵双曲线焦点F到实轴的一个端点的距离等于9,
∴c+a=9…②或c-a=9…③
∴①、②联解,得a=4,c=5;
①、③联解,得a=-4,c=5(舍去)
∴双曲线的离心率e=
=
故选B
∴2b=6⇒b=3⇒c2-a2=32=9…①
又∵双曲线焦点F到实轴的一个端点的距离等于9,
∴c+a=9…②或c-a=9…③
∴①、②联解,得a=4,c=5;
①、③联解,得a=-4,c=5(舍去)
∴双曲线的离心率e=
| c |
| a |
| 5 |
| 4 |
故选B
点评:本题以一个特殊双曲线求离心率为例,着重考查了双曲线的基本概念和离心率等知识点,属于基础题.

练习册系列答案
相关题目


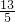

 B.
B. C.
C. D.
D.