题目内容
已知等比数列{an}的前n项和为Sn,若S =4(a1+a3+a5+…+a2n-1),a1a2a3=27,则a6=( )
=4(a1+a3+a5+…+a2n-1),a1a2a3=27,则a6=( )
| A.27 | B.81 | C.243 | D.729 |
C
解析试题分析:利用等比数列的性质可得a1a2a3=a2 =27,解得a2=3,因为S
=27,解得a2=3,因为S =4(a1+a3+a5+…+a2n-1),
=4(a1+a3+a5+…+a2n-1),
所以n=1时,则S2=a1+a2=4a1,从而可得 ,所以
,所以 =243,故选C.
=243,故选C.
考点:1.等比数列的性质;2.等比数列的通项公式.

练习册系列答案
相关题目
等比数列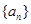 中,已知对任意正整数
中,已知对任意正整数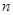 ,
,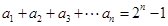 ,则
,则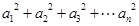 等于( )
等于( )
A.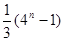 | B.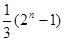 | C.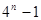 | D.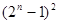 |
已知等比数列 满足
满足 ,且
,且 ,则当
,则当 时,
时, ( )
( )
A. | B. | C. | D. |
等比数列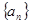 中,
中, 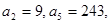 则
则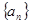 的前4项和为( )
的前4项和为( )
| A.81 | B.120 | C.168 | D.192 |
已知等比数列 的公比为正数,且
的公比为正数,且 ·
· =2
=2 ,
, =1,则
=1,则 = ( )
= ( )
A. | B. | C.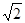 | D.2 |
在正项等比数列 中,已知
中,已知 ,则
,则 的最小值为( )
的最小值为( )
| A.64 | B.32 | C. 16 | D.8 |
等比数列 的各项为正,公比
的各项为正,公比 满足
满足 ,则
,则 的值为 ( )
的值为 ( )
A. | B.2 | C. | D. |
已知数列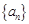 是公比为
是公比为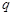 的等比数列,且
的等比数列,且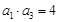 ,
,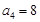 ,则
,则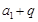 的值为( )
的值为( )
A.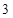 | B.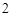 | C.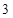 或 或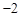 | D.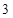 或 或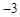 |
在各项都为正数的等比数列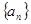 中,首项
中,首项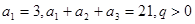 ,则
,则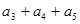 为 ( )
为 ( )
| A.21 | B.4 | C.84 | D.8 |