Question

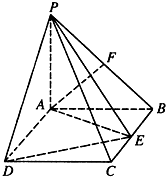如图，PA⊥平面ABCD，四边形ABCD为矩形，PA=AB=

3

，AD=1，点F是PB的中点，点E在边BC上移动．
（Ⅰ）求三棱锥E-PAD的体积；
（Ⅱ）试问当点E在BC的何处时，有EF∥平面PAC；
（Ⅲ）证明：无论点E在边BC的何处，都有PE⊥AF．

Answer 1

分析：（I）由PA⊥平面ABCD，可证AB⊥PA，又AB⊥AD，可证AB⊥平面PAD，求出棱锥的底面面积与高，代入体积公式计算；
（II）当点E是BC的中点时，EF∥PC，再由线线平行证明线面平行；
（III）利用线线垂直证明AF⊥平面PBC．

解答：解（I）∵PA⊥平面ABCD且AC，AB，BC?平面ABCD，

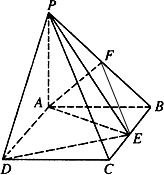
∴PA⊥AC，PA⊥AB，PA⊥BC
∴Rt△PAD中，PA=

3

，AD=1
∴S△PAD=

1

2

×AD×PA=

3

2

又四边形ABCD为矩形，∴AD⊥AB
又AD和PA是面PAD上两相交直线
∴AB⊥平面PAD，又AD∥BC，∴AB就是三棱锥E-PAD的高．
∴VE-PAD=

1

3

×S△PAD×AB=

1

3

×

3

2

×

3

=

1

2

；
（ II）当点E是BC的中点时，有EF∥平面PAC，证明如下：
连结AC，EF
∵点E、F分别是边BC、PB的中点
∴△PBC中，EF∥PC，
又EF?平面PAC，PC?平面PAC，
∴当点E是BC的中点时，EF∥平面PAC，
（III）∵PA⊥AB，PA=AB=

3

，点F是PB的中点
∴等腰△PAB中，AF⊥PB
又PA⊥BC，AB⊥BC且PA和AB是平面PAB上两相交直线
∴BC⊥平面PAB，又AF?平面PAB，
∴AF⊥BC
又PB和BC是平面PBC上两相交直线
∴AF⊥平面PBC，又PE?平面PBC，∴AF⊥PE
∴无论点E在边BC的何处，都有PE⊥AF成立．

点评：本题考查了线面平行的证明，线面垂直的证明，考查了学生的空间想象能力与推理论证能力，关键是要熟练掌握定理的条件．